Covariate Assisted Principal (CAP ) Regression for Matrix Outcomes
Xi (Rossi) LUO
Health Science Center
School of Public Health
Dept of Biostatistics
and Data Science
ABCD Research Group

March 15, 2021
Funding: NIH R01EB022911; NSF/DMS (BD2K) 1557467
Co-Authors

Yi Zhao
Indiana Univ

Bingkai Wang
Johns Hopkins Biostat

Johns Hopkins Medicine

Brian Caffo
Johns Hopkins Biostat
Slides viewable on web:
bit.ly /capenar21
Statistics/Data Science Focuses
Motivating Example

Brain network connections vary by covariates (e.g. age/sex)
Resting-state fMRI Networks
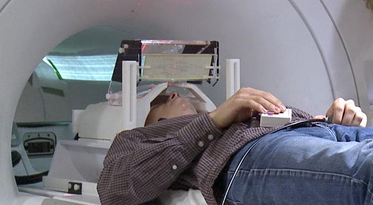
- fMRI measures brain activities over time
- Resting-state: "do nothing" during scanning
- Brain networks constructed using
cov/cor matrices of time series
Mathematical Problem
- Given $n$ (semi-)positive matrix outcomes, $\Sigma_i\in \real^{p\times p}$
- Given $n$ corresponding vector covariates, $x_i \in \real^{q}$
- Find function $g(\Sigma_i) = x_i \beta$, $i=1,\dotsc, n$
- In essense,
regress positive matrices on vectors
Some Related Problems
- Heterogeneous regression or weighted LS:
- Usually for scalar variance $\sigma_i$, find $g(\sigma_i) = f(x_i)$
- Goal: to improve efficiency, not to interpret $x_i \beta$
- Covariance models Anderson, 73; Pourahmadi, 99; Hoff, Niu, 12; Fox, Dunson, 15; Zou, 17
- Model $\Sigma_i = g(x_i)$, sometimes $n=i=1$
- Goal: better models for $\Sigma_i$
- Multi-group PCA Flury, 84, 88; Boik 02; Hoff 09; Franks, Hoff, 16
- No regression model, cannot handle vector $x_i$
- Goal: find common/uncommon parts of multiple $\Sigma_i$
- Tensor-on-scalar regression Li, Zhang, 17; Sun, Li, 17
- No guarantees for positive matrix outcomes
Massive Edgewise Regressions
- Intuitive method by mostly neuroscientists
- Try $g_{j,k}(\Sigma_i) = \Sigma_{i}[j,k] = x_i \beta$
- Repeat for all $(j,k) \in \{1,\dotsc, p\}^2$ pairs
- Essentially $O(p^2)$ regressions for each connection
- Limitations: multiple testing $O(p^2)$, failure to accout for dependencies between regressions
Our CAP in a Nutshell
$\mbox{PCA}(\Sigma_i) = x_i \beta$
- Essentially, we aim to turn unsupervised PCA to a supervised PCA
- Ours differs from existing PCA methods:
- Supervised PCA Bair et al, 06 models
scalar-on-vector
- Supervised PCA Bair et al, 06 models
Other Extensions
- Our regression framework for covariance matrix outcomes is flexbile
- The framework paper published in Biostatistics 2020
- Easily extended to voxel-level covariance matrices Brain and Behavior, Accepted
- Many other extensions under review or preparation: high dimensional, mixed effects, ...
Model and Method
Model
- Find principal direction (PD) $\gamma \in \real^p$, such that: $$ \log({\gamma}^\top\Sigma_{i}{\gamma})=\beta_{0}+x_{i}^\top{\beta}_{1}, \quad i =1,\dotsc, n$$
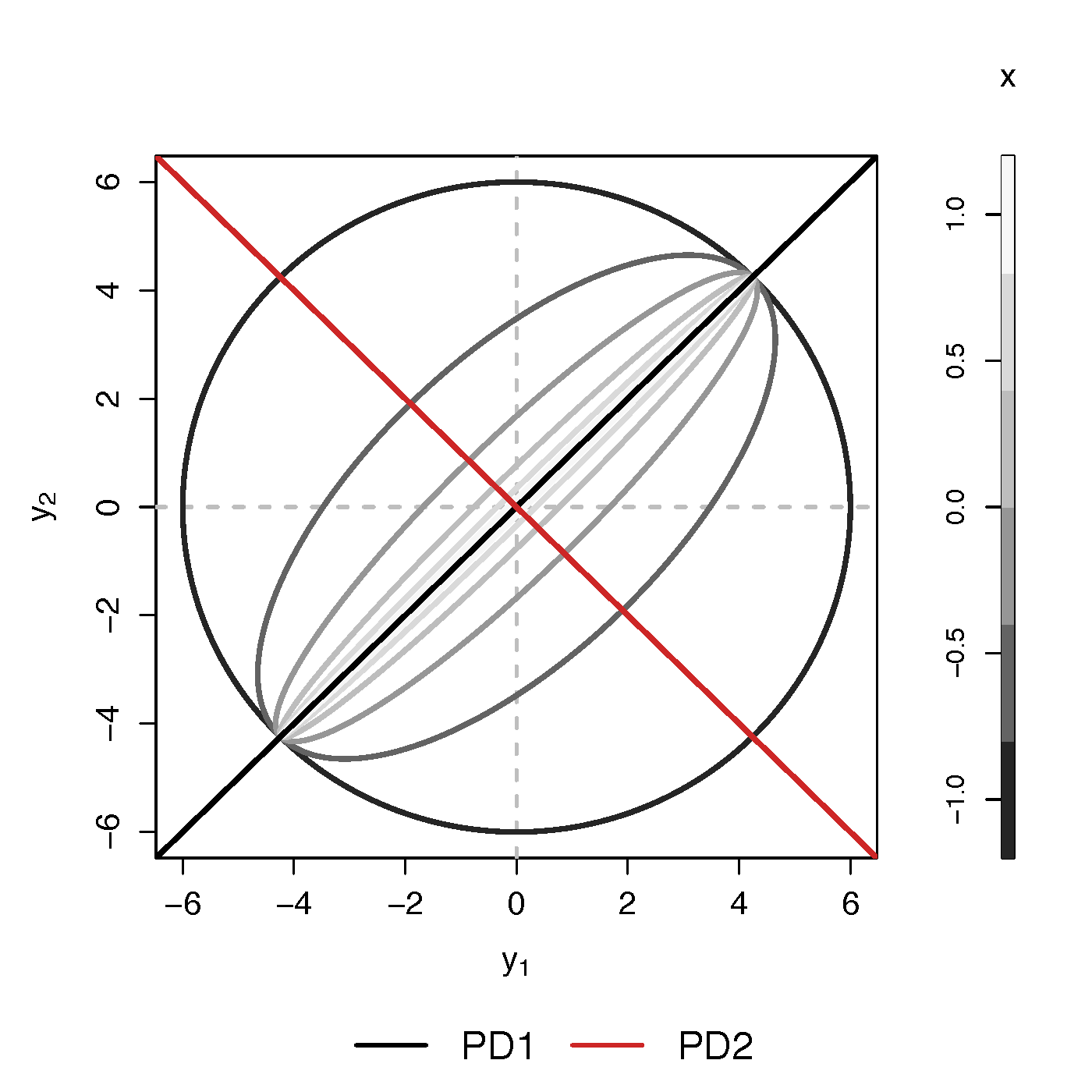
Example (p=2): PD1 largest variation but not related to $x$
PCA selects PD1, Ours selects
Advantages
- Scalability: potentially for $p \sim 10^6$ or larger
- Interpretation: covariate assisted PCA
- Turn
unsupervised PCA intosupervised
- Turn
- Sensitivity: target those covariate-related variations
Covariate assisted SVD?
- Applicability: other big data problems besides fMRI
Method
- MLE with constraints: $$\scriptsize \begin{eqnarray}\label{eq:obj_func} \underset{\boldsymbol{\beta},\boldsymbol{\gamma}}{\text{minimize}} && \ell(\boldsymbol{\beta},\boldsymbol{\gamma}) := \frac{1}{2}\sum_{i=1}^{n}(x_{i}^\top\boldsymbol{\beta}) \cdot T_{i} +\frac{1}{2}\sum_{i=1}^{n}\boldsymbol{\gamma}^\top \Sigma_{i}\boldsymbol{\gamma} \cdot \exp(-x_{i}^\top\boldsymbol{\beta}) , \nonumber \\ \text{such that} && \boldsymbol{\gamma}^\top H \boldsymbol{\gamma}=1 \end{eqnarray}$$
- Two obvious constriants:
- C1: $H = I$
- C2: $H = n^{-1} (\Sigma_1 + \cdots + \Sigma_n) $
Choice of $H$
Will focus on the constraint (C2)
Algoirthm
- Iteratively update $\beta$ and then $\gamma$
- Prove explicit updates
- Extension to multiple $\gamma$:
- After finding $\gamma^{(1)}$, we will update $\Sigma_i$ by removing its effect
- Search for the next PD $\gamma^{(k)}$, $k=2, \dotsc$
- Impose the orthogonal constraints such that $\gamma^{k}$ is orthogonal to all $\gamma^{(t)}$ for $t\lt k$
Theory for $\beta$
Theory for $\gamma$
Simulations
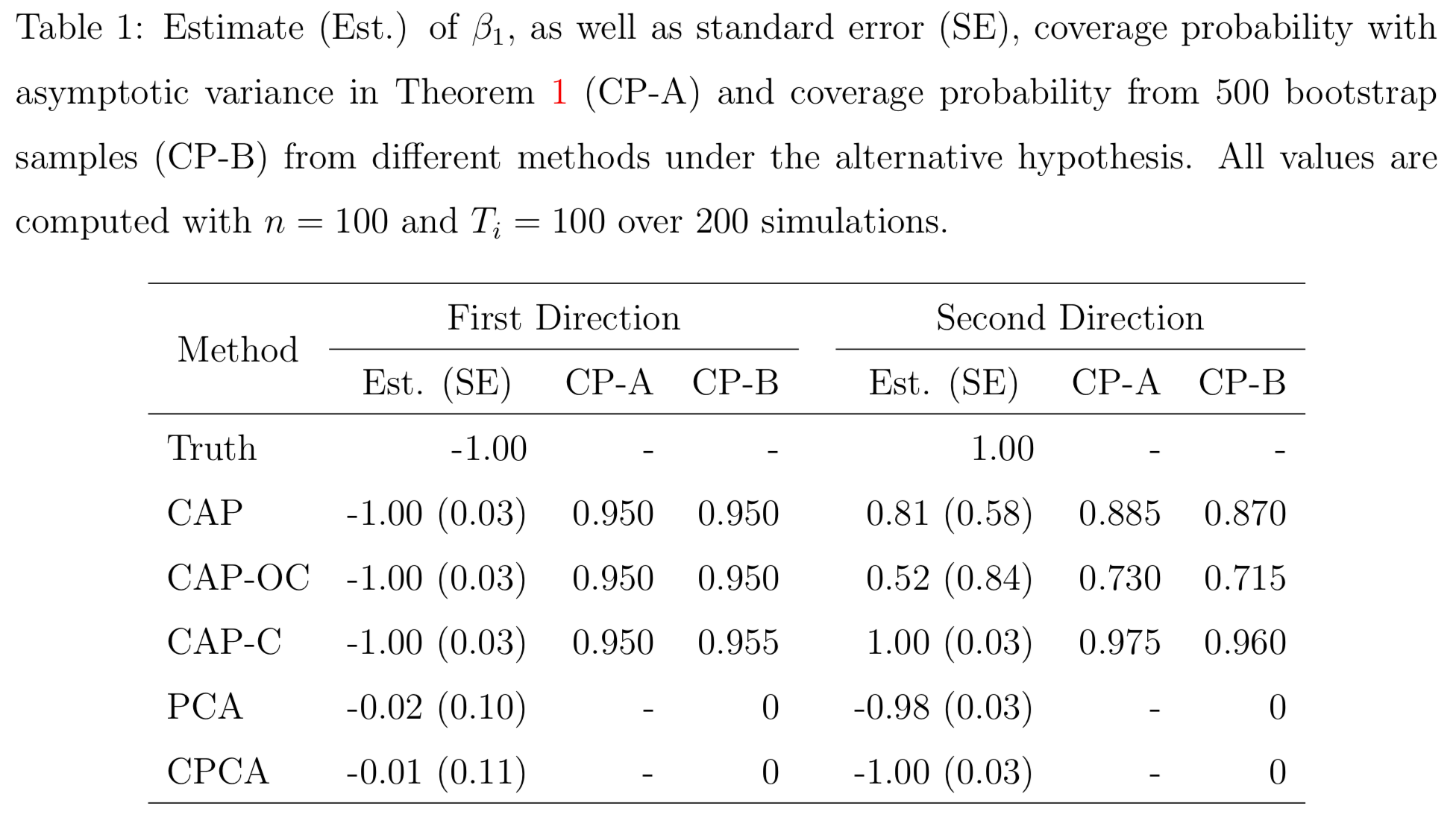
PCA and common PCA do not find the first principal direction, because they don't model covariates
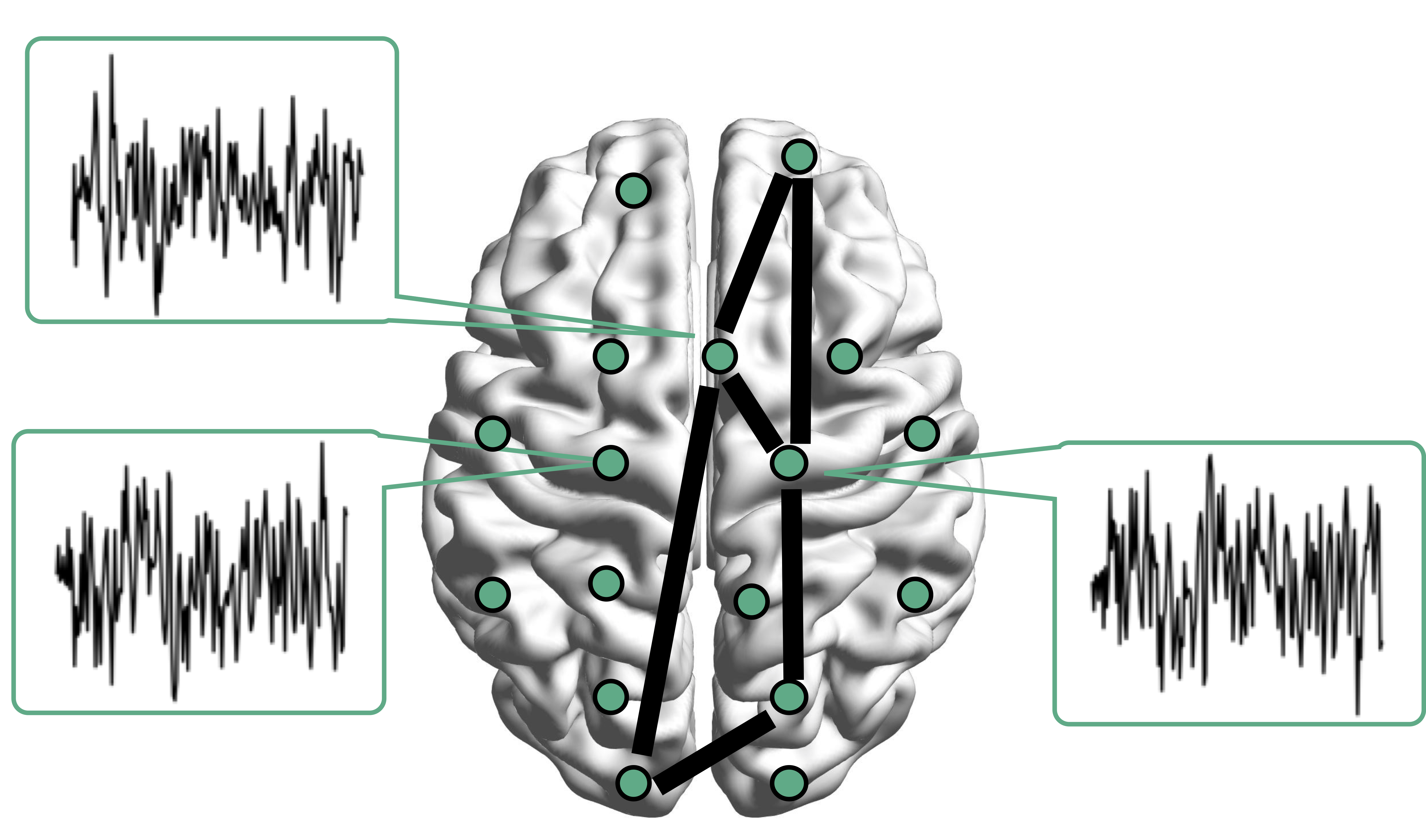
Resting-state fMRI
Regression Coefficients
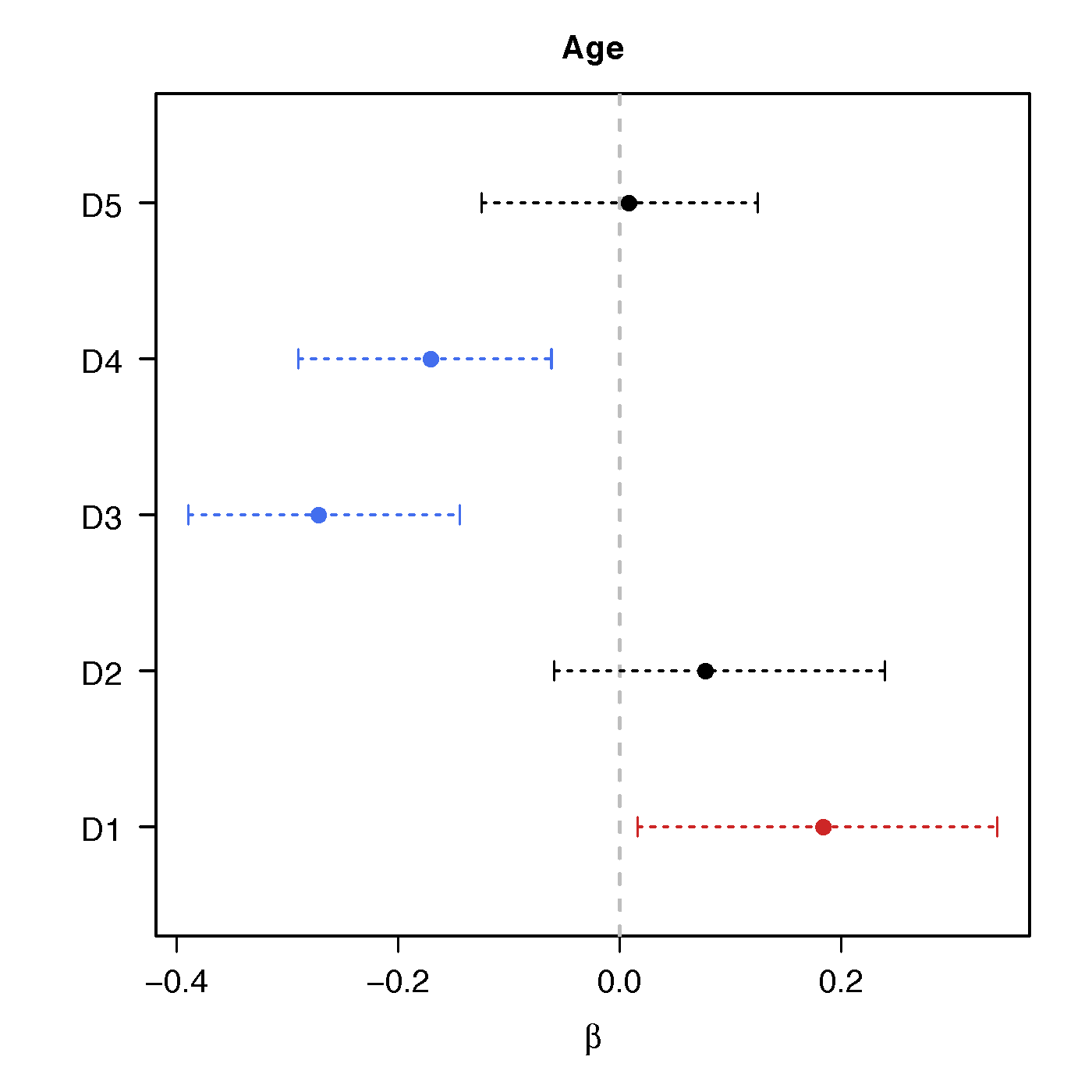
Age
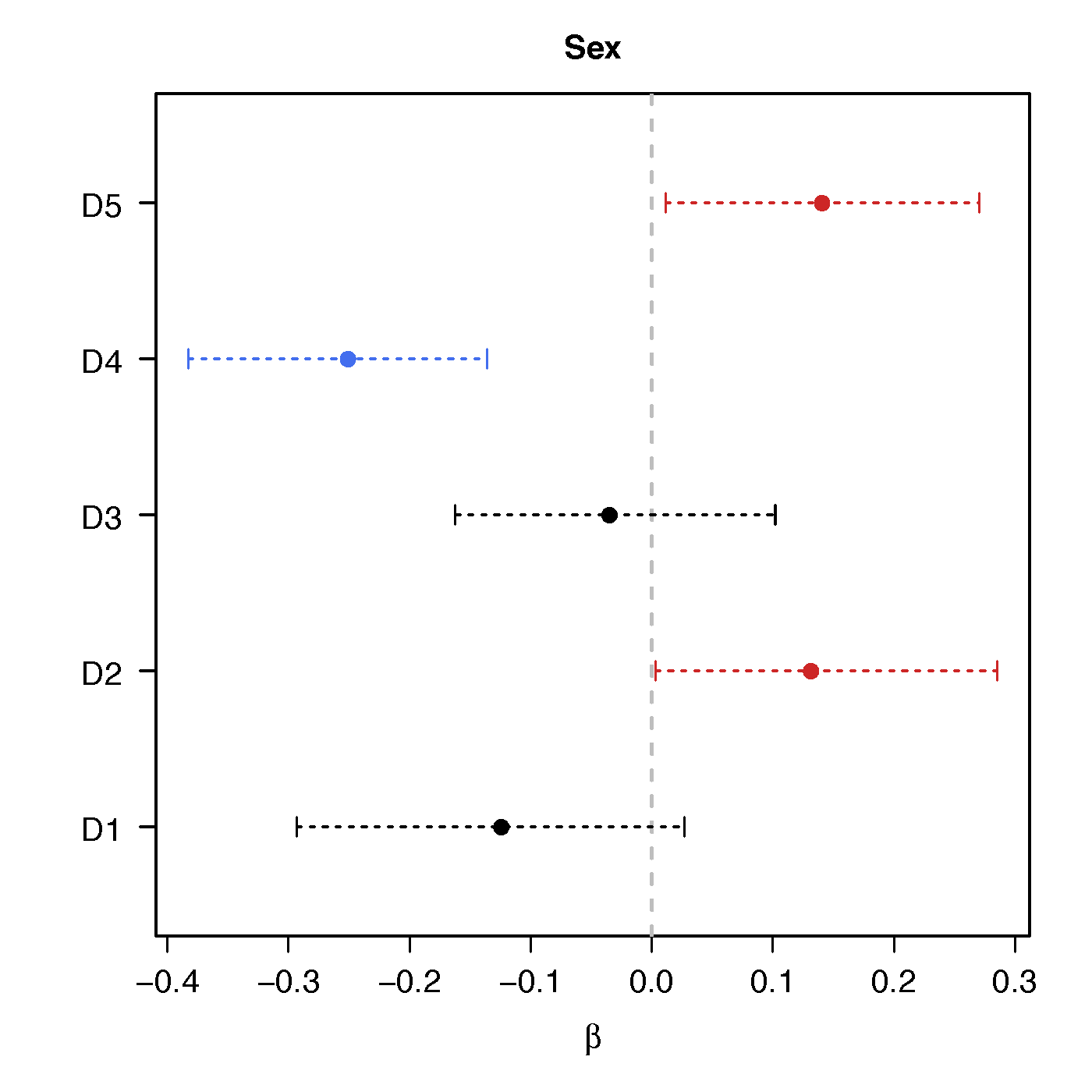
Sex
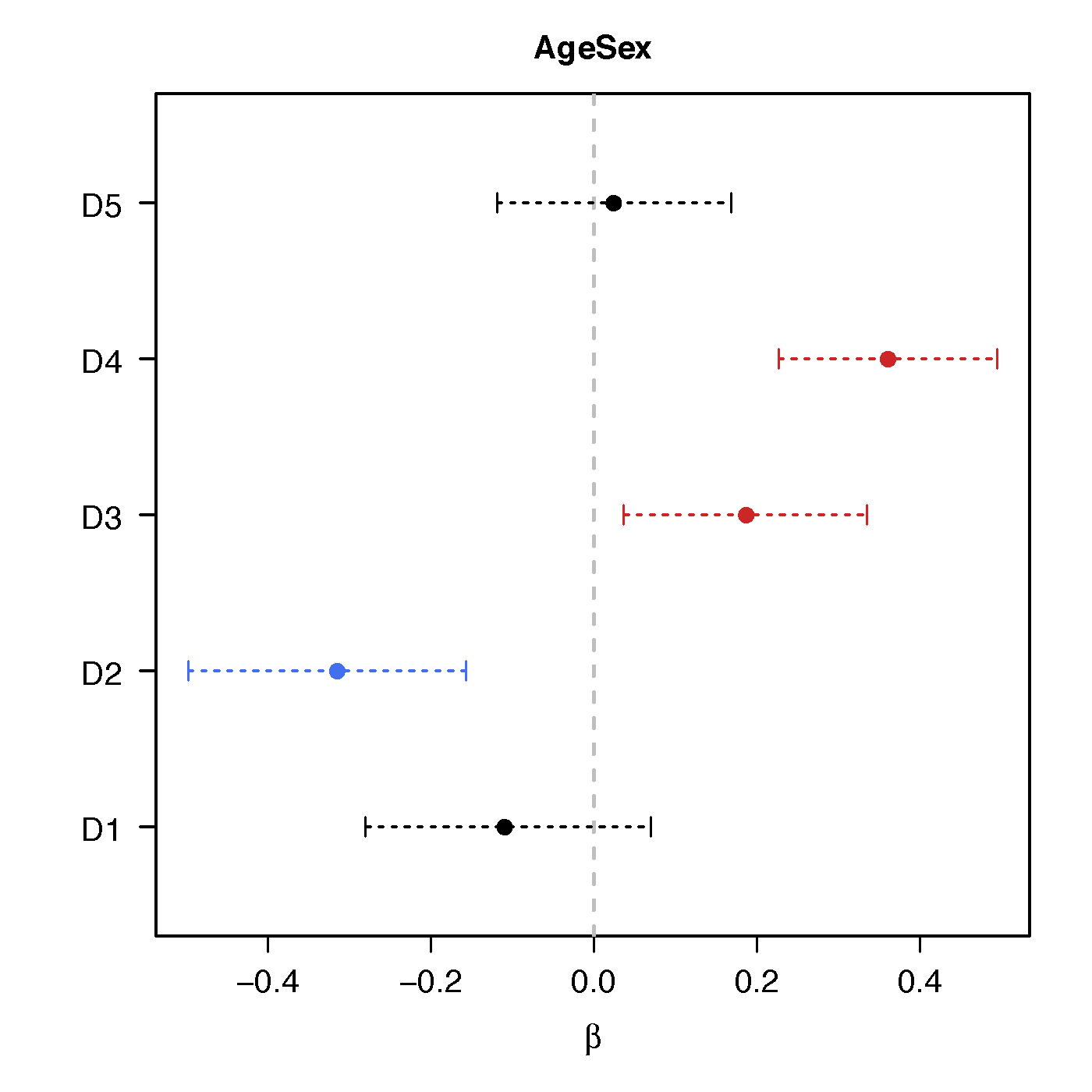
Age*Sex
No statistical significant changes were found by massive edgewise regression
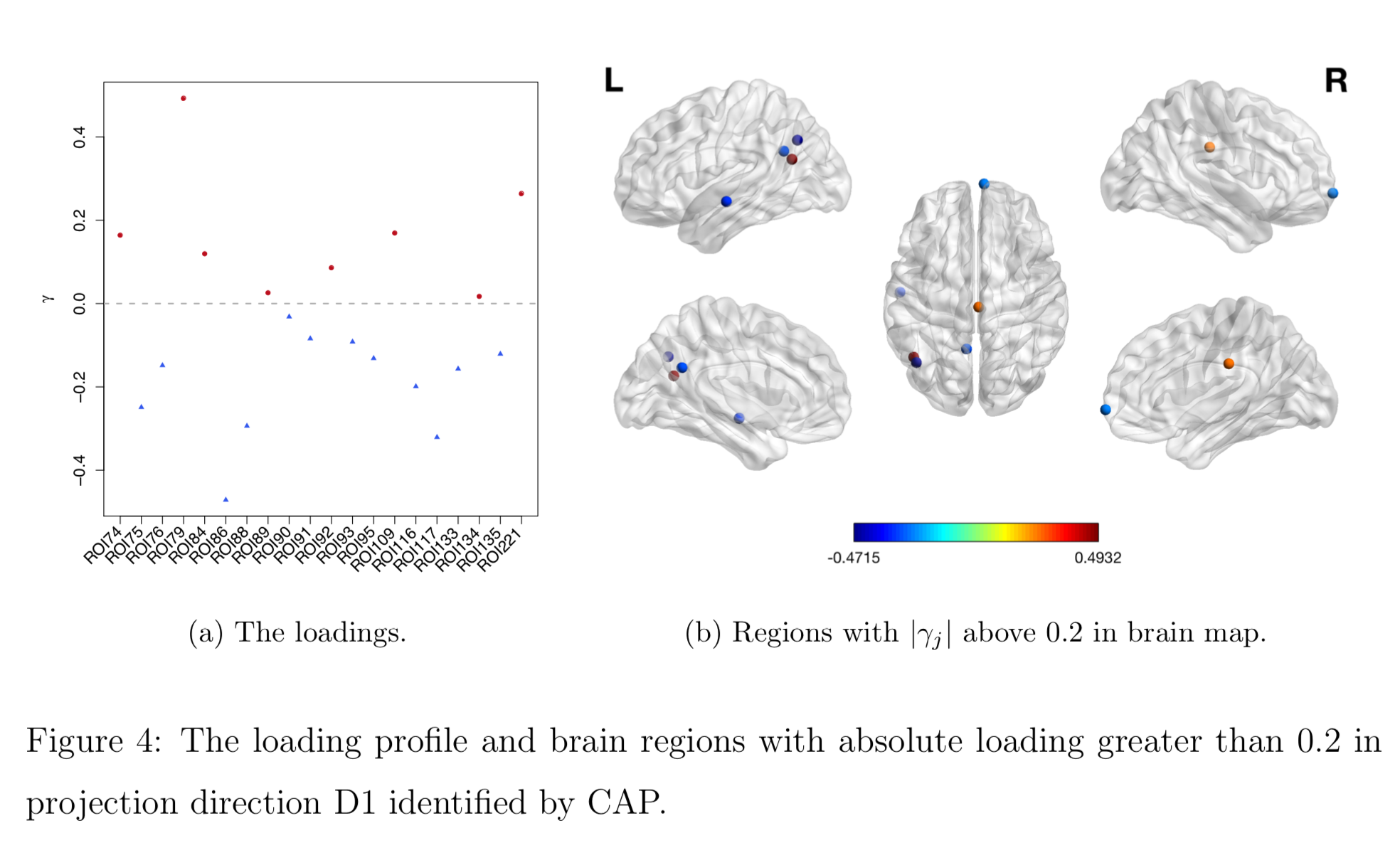
Brain Map of $\gamma$
Discussion
- Regress
PD matrices on vectors - Method to identify covariate-related (supervised) directions vs (unsupervised) PCA
- Theorectical justifications
- Paper: Biostatistics (10.1093/biostatistics/kxz057)
- R pkg:
cap 
Thank you!
Comments? Questions?
BigComplexData.com
or BrainDataScience.com