Covariance/Network Outcome Modeling via Covariate A ssisted Principal (CAP) Regression


Xi (Rossi) LUO


The University of Texas
Health Science Center
School of Public Health
Dept of Biostatistics
and Data Science
ABCD Research Group 


Univ of Houston, Dept of Mathematics
April 24, 2023

Funding: NIH R01MH126970, R01EB022911; NSF/DMS 1557467

Major Collaborators

Yi Zhao

Yi Zhao
Indiana Univ

Bingkai Wang

Bingkai Wang
UMich Biostat

Stewart Mostofsky

Chiang-shan Ray Li
Yale Univ

Stewart Mostofsky

Stewart Mostofsky
Johns Hopkins Medicine

Brian Caffo

Brian Caffo
Johns Hopkins Biostat

Slides viewable on web:
bit.ly/capuh23

Statistics/Data Science Focuses

Resting-state fMRI Networks

  • fMRI measures brain activities over time
  • Resting-state: "do nothing" during scanning


  • Brain networks constructed using cov/cor matrices of time series

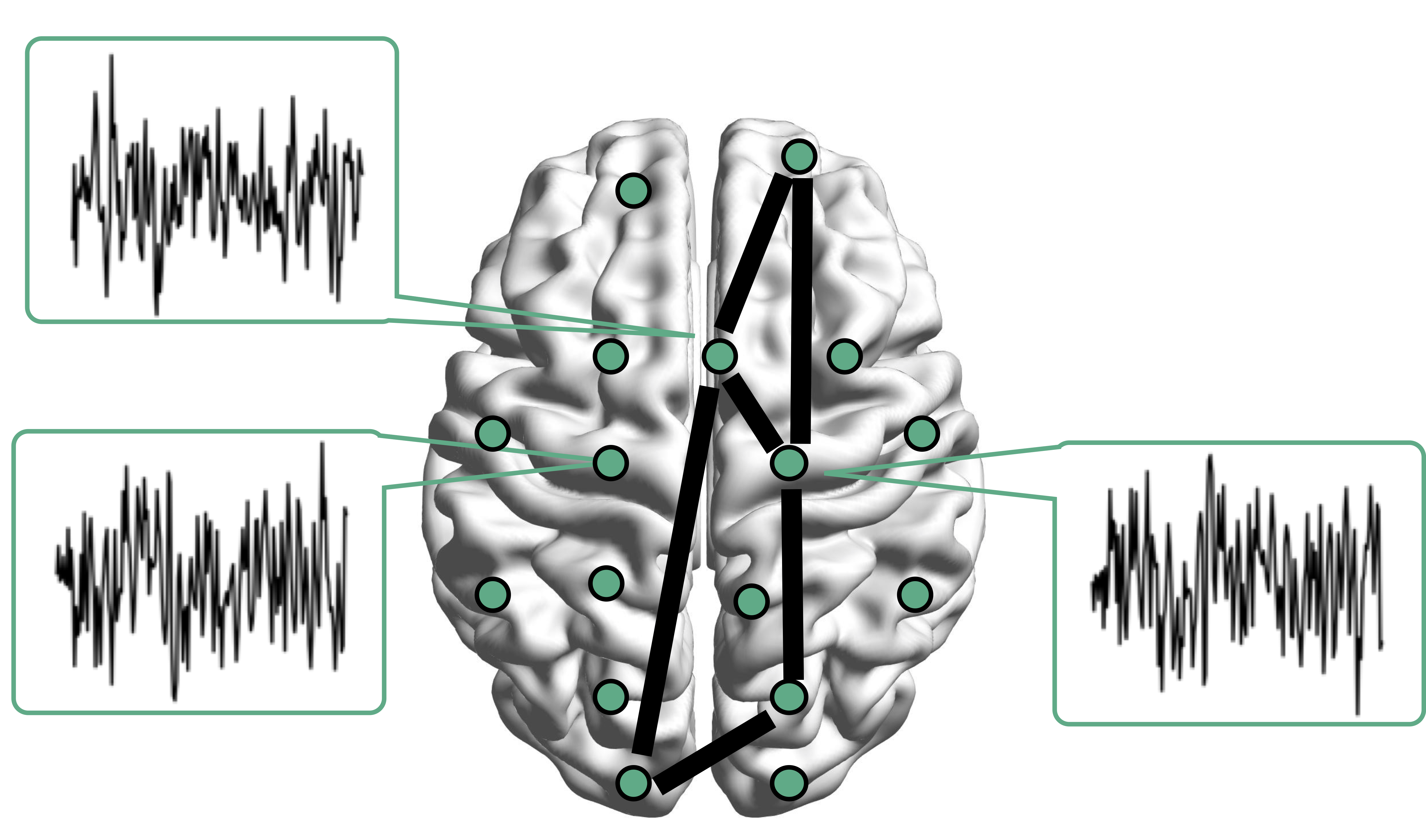
fMRI data: blood-oxygen-level dependent (BOLD) signals from each cube. Each subject: observe matrix regions $\times$ time

Brain Networks

  • Brain network analysis: an emerging trend Park, Friston, Science, 2013
  • Estimating brain networks from data
    • Many methodological frameworks: cov, inv cov, DCM, Granger,ICA, frenquency, dynamic...
    • Our group worked on graphical models Cai et al, 2001, Liu, L, 2015, DCM Cao et al, 2019
  • Also on quantifying network info flow Zhao, L, 2019, Zhao L, 2021
  • On utilization of networks for clustering Bunea et al, 2020
  • Tree-like networks and regression Wang et al, 2022; Zhao et al, In Press
  • This talk: explaining network differences

Motivating Example

Brain network connections vary by covariates (e.g. age/sex)


Goal: model how covariates change network connections

Our Idea

$$\textrm{function}(\textbf{graph}) = \textbf{age}\times \beta_1 + \textbf{sex}\times \beta_2 + \cdots $$

Other Related Applications

  • Differences in genetic networks
    • Networks by disease/age/sex groups
    • Single cell sequencing
  • Covariance modeling
    • Temporal changes in covariance matrices
    • Spatial-temporal
  • Theme: signals in the second moment, low/no signals in the first moment

Mathematical Problem

  • Given $n$ (semi-)positive matrices, $\Sigma_i\in \real^{p\times p}$
  • Given $n$ corresponding vector covariates, $x_i \in \real^{q}$
  • Find function $g(\Sigma_i) = x_i \beta$, $i=1,\dotsc, n$
  • In essense, regress positive matrices on vectors

Other Extensions


  • Linear model formulation, and thus very flexible
  • Easily extended to big data with 1 million brain regions, Brain and Behavior
  • High dim cov (later), Electronic J of Stat
  • Many other extensions under review or preparation: longitudinal, mixed effects, ...

Some Related Problems

  • Heterogeneous regression or weighted LS:
    • Usually for scalar variance $\sigma_i$, find $g(\sigma_i) = f(x_i)$
    • Goal: to improve efficiency, not to interpret $x_i \beta$
  • Covariance models Anderson, 73; Pourahmadi, 99; Hoff, Niu, 12; Fox, Dunson, 15; Zou, 17
    • Model $\Sigma_i = g(x_i)$, sometimes $n=i=1$
    • Goal: better models for $\Sigma_i$
  • Multi-group PCA, (inverse) covariance estimation/testing Flury, 84, 88; Boik 02; Hoff 09; Franks, Hoff, 16, Guo et al, 11; Tsai et al, 22; Cai et al, 13
    • No regression model, cannot handle vector $x_i$
    • Goal: find common/uncommon parts of multiple (inv) $\Sigma_i$
  • Tensor-on-scalar regression Li, Zhang, 17; Sun, Li, 17
    • No guarantees for positive matrix outcomes

CAP for Low-dimensional Cov Outcomes

Naive: Massive Edgewise Regressions

  • Intuitive method by mostly neuroscientists
  • Try $g_{j,k}(\Sigma_i) = \Sigma_{i}[j,k] = x_i \beta$
  • Repeat for all $(j,k) \in \{1,\dotsc, p\}^2$ pairs
  • Essentially $O(p^2)$ regressions for each connection
  • Limitations:
    • multiple testing $O(p^2)$
    • failure to accout for dependencies between regressions
    • low signal to noise ratio elementwise, spectral modeling may be more robust

Our CAP in a Nutshell


$\mbox{Modified PCA}(\Sigma_i) = x_i \beta$

  • Essentially, we aim to turn unsupervised PCA to a supervised PCA
  • Ours differs from existing PCA methods:
    • Supervised PCA Bair et al, 06 models scalar-on-vector

Model and Method

Model

  • Find principal direction (PD) $\gamma \in \real^p$, such that: $$ \log({\gamma}^\top\Sigma_{i}{\gamma})=\beta_{0}+x_{i}^\top{\beta}_{1}, \quad i =1,\dotsc, n$$

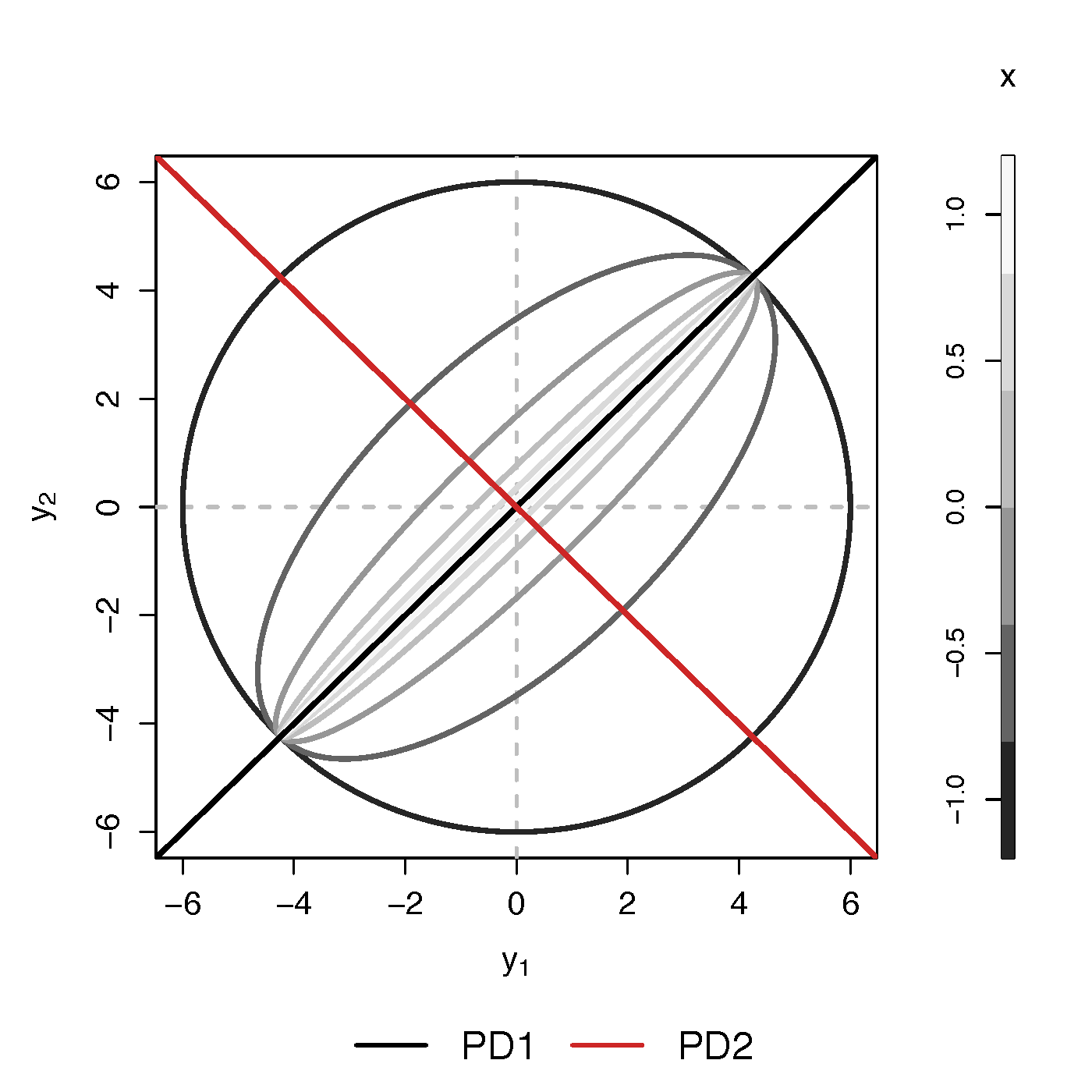
Example (p=2): PD1 largest variation in $\Sigma_i$ but not related to $x$

PCA selects PD1, Ours selects PD2

Advantages

  • Scalability: potentially for $p \sim 10^6$ or larger
  • Interpretation: covariate assisted PCA
    • Turn unsupervised PCA into supervised
  • Sensitivity: target those covariate-related variations
    • Covariate assisted SVD?
  • Potential applications in other big data problems besides fMRI

Method

  • MLE with constraints: $$\scriptsize \begin{eqnarray}\label{eq:obj_func} \underset{\boldsymbol{\beta},\boldsymbol{\gamma}}{\text{minimize}} && \ell(\boldsymbol{\beta},\boldsymbol{\gamma}) := \frac{1}{2}\sum_{i=1}^{n}(x_{i}^\top\boldsymbol{\beta}) \cdot T_{i} +\frac{1}{2}\sum_{i=1}^{n}\boldsymbol{\gamma}^\top \Sigma_{i}\boldsymbol{\gamma} \cdot \exp(-x_{i}^\top\boldsymbol{\beta}) , \nonumber \\ \text{such that} && \boldsymbol{\gamma}^\top H \boldsymbol{\gamma}=1 \end{eqnarray}$$
  • No meaningful solutions without constraints
  • Two obvious constriants:
    • C1: $H = I$
    • C2: $H = n^{-1} (\Sigma_1 + \cdots + \Sigma_n) $
  • The most natural C1 usually does not work!

Choice of $H$

Proposition: When (C1) $H=\boldsymbol{\mathrm{I}}$ in the optimization problem, for any fixed $\boldsymbol{\beta}$, the solution of $\boldsymbol{\gamma}$ is the eigenvector corresponding to the minimum eigenvalue of matrix $$ \sum_{i=1}^{n}\frac{\Sigma_{i}}{\exp(x_{i}^\top\boldsymbol{\beta})} $$

  • C1 leads to small eigen values (potential noises)
  • Will focus on the constraint (C2)

Algoirthm

  • Iteratively update $\beta$ and then $\gamma$
  • Prove explicit updates (see our papers)
  • Extension to multiple $\gamma$:
    • After finding $\gamma^{(1)}$, we will update $\Sigma_i$ by removing its effect
    • Search for the next PD $\gamma^{(k)}$, $k=2, \dotsc$
    • Impose the orthogonal constraints such that $\gamma^{k}$ is orthogonal to all $\gamma^{(t)}$ for $t\lt k$

Theory for $\beta$

Theorem: Assume $\sum_{i=1}^{n}x_{i}x_{i}^\top/n\rightarrow Q$ as $n\rightarrow\infty$. Let $T=\min_{i}T_{i}$, $M_{n}=\sum_{i=1}^{n}T_{i}$, under the true $\boldsymbol{\gamma}$, we have \begin{equation} \sqrt{M_{n}}\left(\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}\right)\overset{\mathcal{D}}{\longrightarrow}\mathcal{N}\left(\boldsymbol{\mathrm{0}},2 Q^{-1}\right),\quad \text{as } n,T\rightarrow\infty, \end{equation} where $\hat{\boldsymbol{\beta}}$ is the maximum likelihood estimator when the true $\boldsymbol{\gamma}$ is known.

Theory for $\gamma$

Theorem: Assume $\Sigma_{i}=\Gamma\Lambda_{i}\Gamma^\top$, where $\Gamma=(\boldsymbol{\gamma}_{1},\dots,\boldsymbol{\gamma}_{p})$ is an orthogonal matrix and $\Lambda_{i}=\mathrm{diag}\{\lambda_{i1},\dots,\lambda_{ip}\}$ with $\lambda_{ik}\neq\lambda_{il}$ ($k\neq l$), for at least one $i\in\{1,\dots,n\}$. There exists $k\in\{1,\dots,p\}$ such that for $\forall~i\in\{1,\dots,n\}$, $\boldsymbol{\gamma}_{k}^\top\Sigma_{i}\boldsymbol{\gamma}_{k}=\exp(x_{i}^\top\boldsymbol{\beta})$. Let $\hat{\boldsymbol{\gamma}}$ be the maximum likelihood estimator of $\boldsymbol{\gamma}_{k}$ in Flury, 84. Then assuming that the assumptions are satisfied,

$\hat{ \boldsymbol{\beta}}$ from our algorithm is $\sqrt{M_{n}}$-consistent estimator of $\boldsymbol{\beta}$.

Simulations


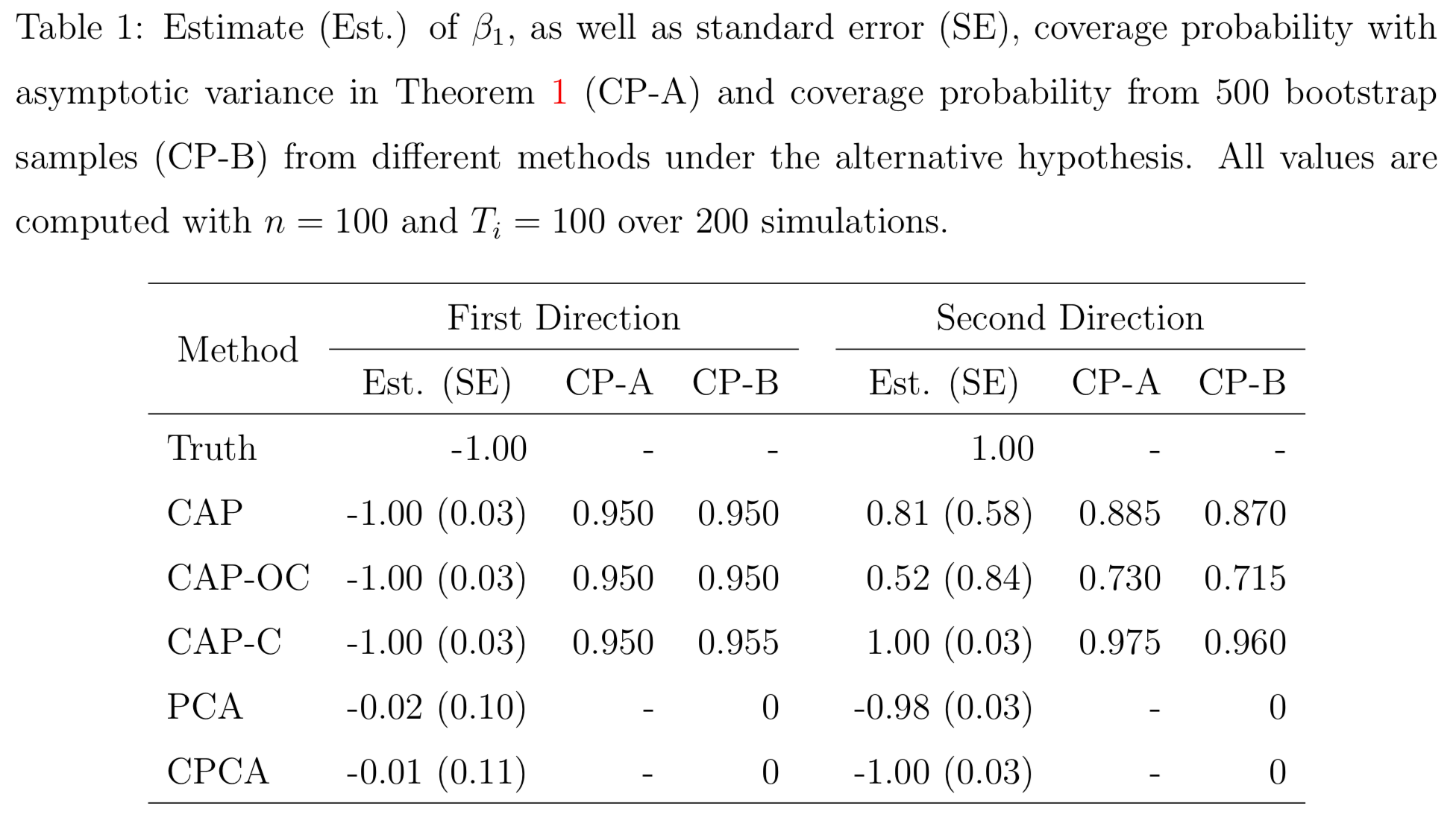
PCA and common PCA do not find the first principal direction, because they don't consider covariates

Resting-state fMRI

Regression Coefficients


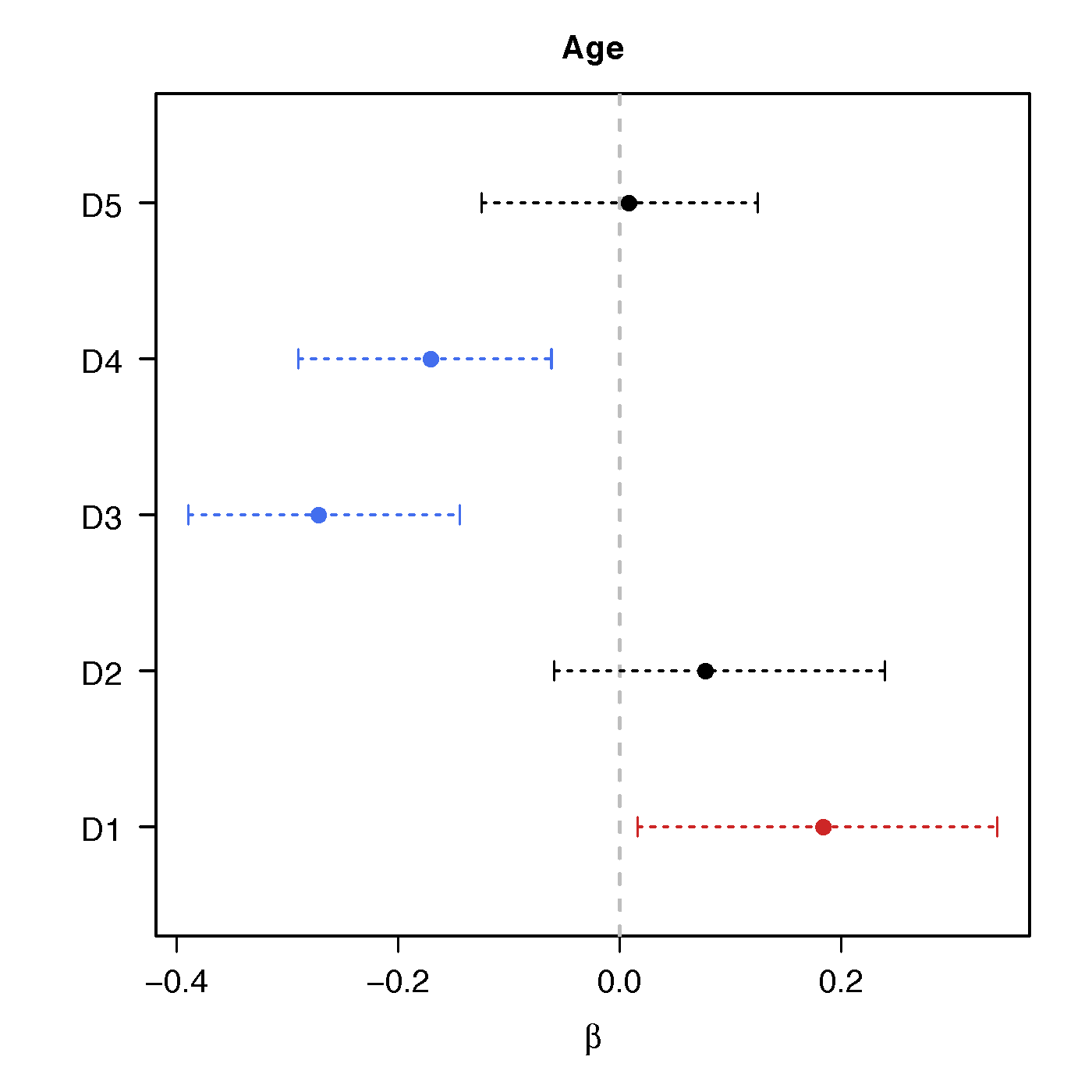
Age

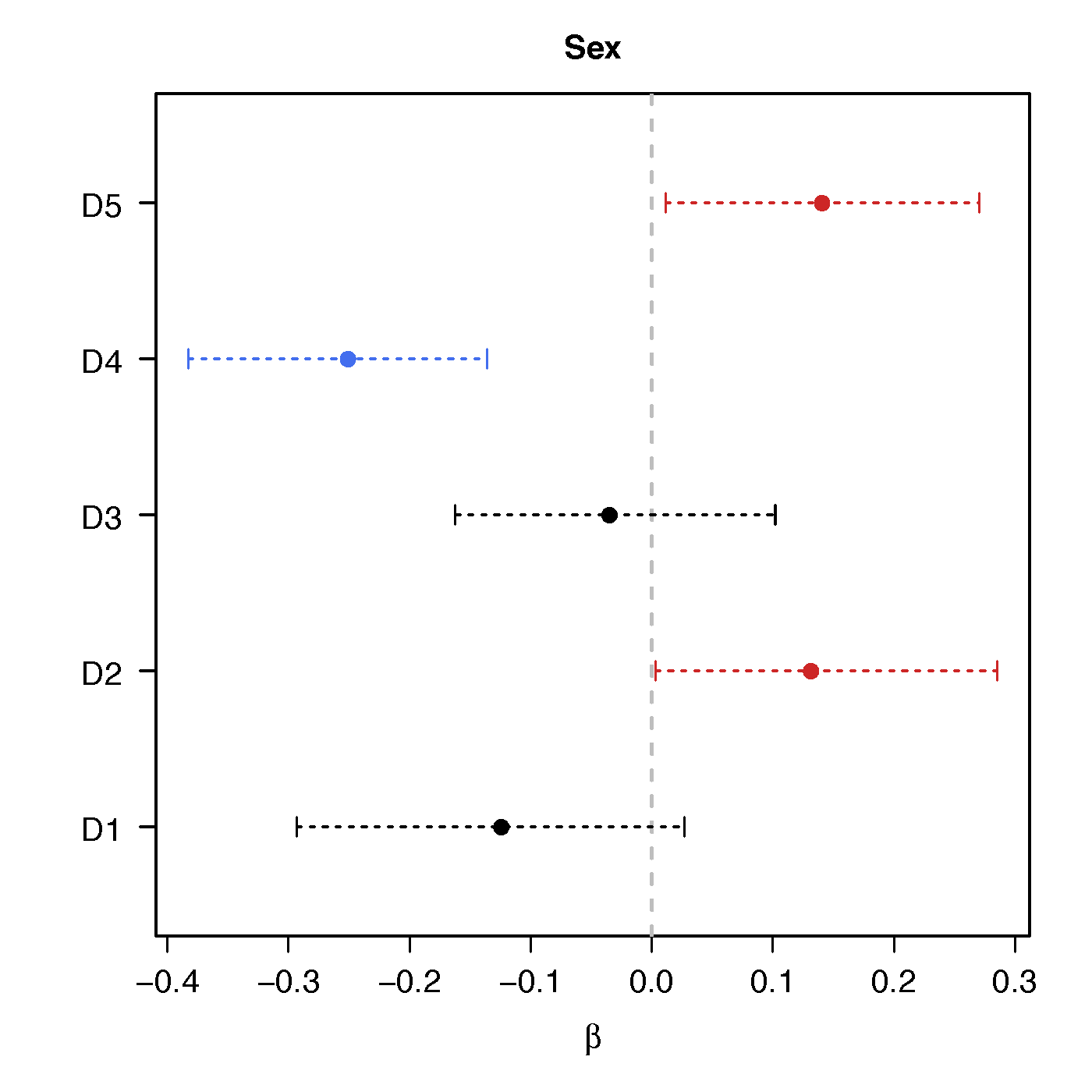
Sex

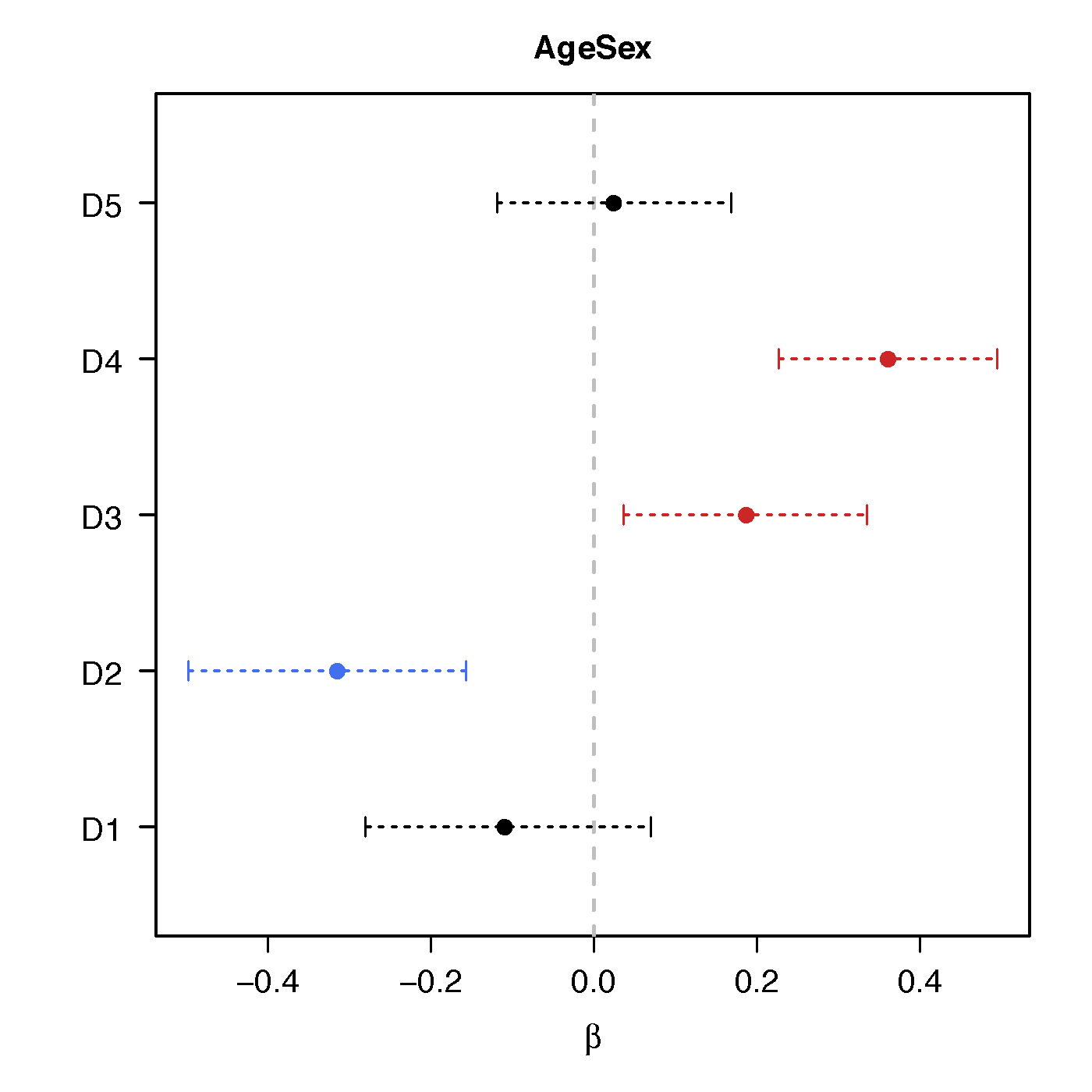
Age*Sex



  • Ours above: significant network differences due to age, sex and their interactions
  • Naive massive edgewise regression: no statistical significant changes in cov entries

Brain Map of $\gamma$

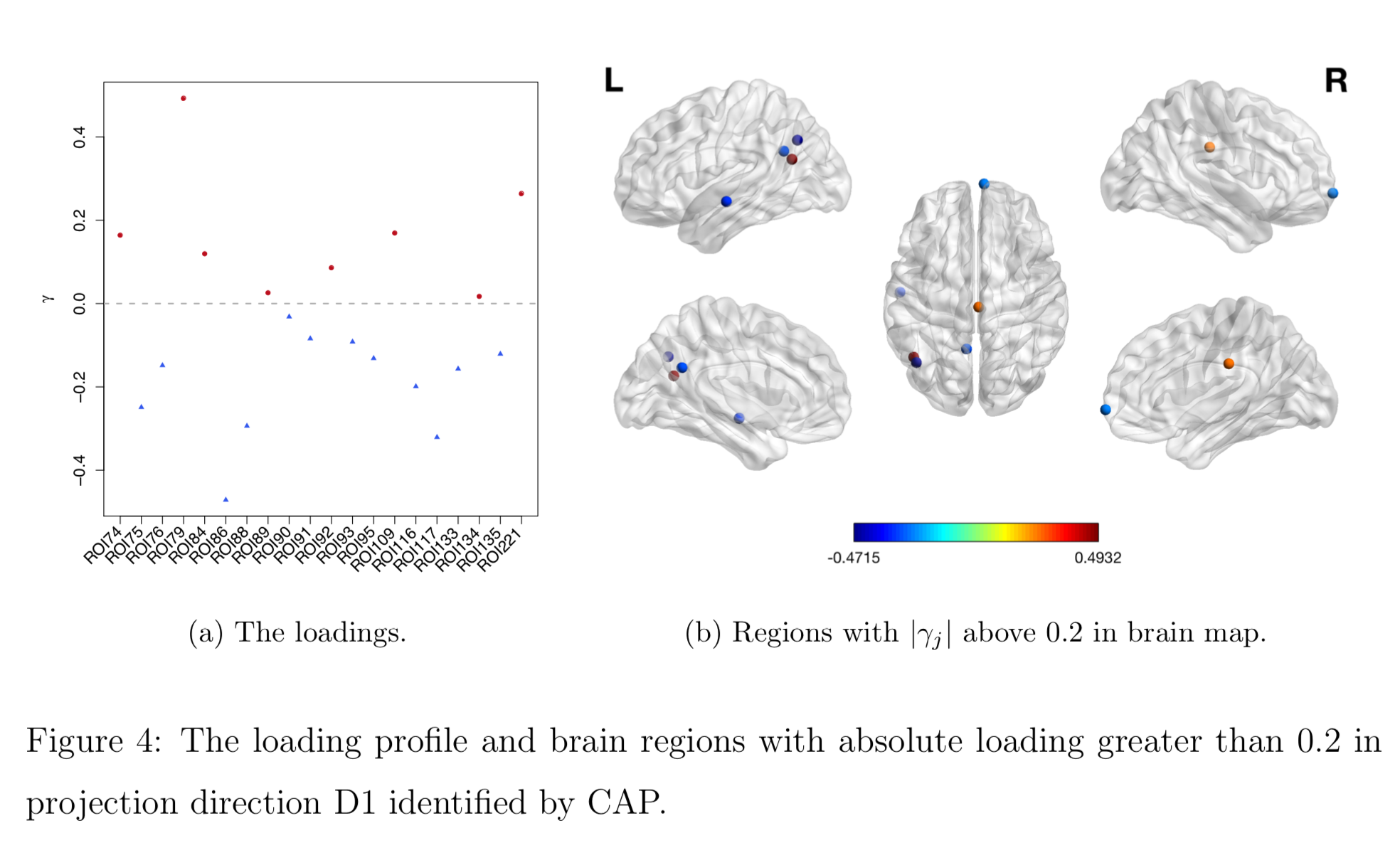
High-Dim Cov Extensions

  • Voxel level (super-high dim) cov matrices Zhao et al, 2020
    • Raw cov: $10^6 \times 10^6$=Trillions of cov elements
    • Decompose data/networks via ICA/PCA
    • Explain netowrk diff on reduced dim
    • Reconstruct brain network maps at the voxel level
  • High dimensional cov Zhao et al, 2021
    • Joint shrinkage Ledoit, Wolf, 2004 of multiple cov
    • Optimum in theory by our joint shrinkage
    • Method/theory also work with joint shrinkage

CAP for High-dimensional Cov Outcomes

Challenges in High-dim

  • Sample covariance not full rank in high-dim: when sample size $T_i$ ≪ variable size $p$
  • $p$ fixed in the previous theory
  • Sample cov is a poor estimator in high dim
  • Eigenvalues even more dispersed
  • Regularization Ledoit, Wolf 04 less optimal

L-W Cov Shrinkage

  • By Ledoit and Wolf (2004), over 2800 citations so far
  • Given sample cov $S$, find estimator $\Sigma^*$ by $$ \begin{eqnarray} \underset{\mu,\rho}{\text{minimize}} && \mathbb{E}\left\| \Sigma^{*}- S \right\|^{2} \nonumber \\ \text{such that} && \Sigma^{*}=\rho\mu\boldsymbol{\mathrm{I}}+(1-\rho)S \end{eqnarray} $$
  • $\rho$ and $\mu$ can be estimated consistently, and thus $\Sigma^*$ consistently
  • Limitations: not handling multiple covariance matrices jointly, not using the covariate info

Our Contributions

  • New joint shrinkage estimator for multiple covariances
  • Incorporate covariate info in regression
  • Minimum quadratic risk asymptotically among all linear combinations, while L-W is suboptimal
  • Also provide consistent estimator for CAP

Covariate Dependent CAP Shrinkage

  • Propose CAP shrinkage by $$ \begin{eqnarray} \underset{\mu,\rho}{\text{minimize}} && \frac{1}{n}\sum_{i=1}^{n}\mathbb{E}\left\{\gamma^\top\Sigma_{i}^{*}\gamma-\exp( x_{i}^\top\beta)\right\}^{2} \nonumber \\ \text{such that} && \Sigma_{i}^{*}=\rho\mu\boldsymbol{\mathrm{I}}+(1-\rho)S_{i}, \quad \text{for } i=1,\dots,n. \end{eqnarray} $$
  • Prove a theorem for solving the optimization and an estimator for $\Sigma_i^*$ $$ S_i^* = \hat{f}(\gamma, x_i, \beta) \boldsymbol{\mathrm{I}} + \hat{g}(\gamma, x_i, \beta) S_i $$ where $S_i^* $ is a consistent estimator, $\hat{f}$ and $\hat{g}$ are computed by explicit formulas from data

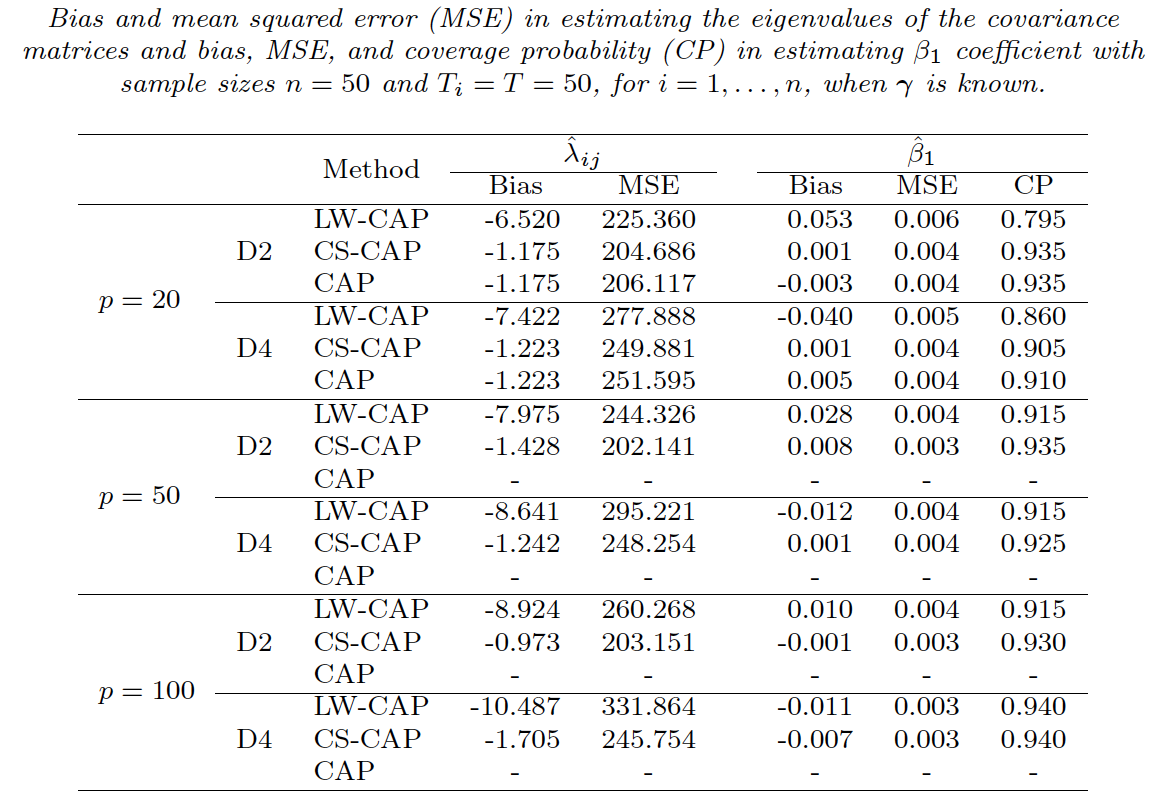
CS-CAP Algorithm

Iteratively update $S^*$, $\gamma$, $\beta$ until cconvergence

Theorem: Assume $(\gamma, \beta)$ is given. With a fixed $n\in\mathbb{N}^{+}$, for any sequence of linear combinations $\{\hat{\Sigma}_{i}\}_{i=1}^{n}$ of the identity matrix and the sample covariance matrix, where the combination coefficients are constant over $i\in\{1,\dots,n\}$, the estimator $ S_{i}^{*}$ verifies: $$ \tiny \begin{equation} \lim_{T\rightarrow\infty}\inf_{T_{i}\geq T}\left[\frac{1}{n}\sum_{i=1}^{n}\mathbb{E}\left\{\gamma^\top\hat{\Sigma}_{i}\gamma-\exp(\bx_{i}^\top \beta)\right\}^{2}-\frac{1}{n}\sum_{i=1}^{n}\mathbb{E}\left\{\gamma^\top S_{i}^{*}\gamma-\exp(\bx_{i}^\top \beta)\right\}^{2}\right]\geq 0. \end{equation} $$ In addition, every sequence of $\{\hat{\Sigma}_{i}\}_{i=1}^{n}$ that performs as well as $\{ S_{i}^{*}\}_{i=1}^{n}$ is identical to $\{ S_{i}^{*}\}_{i=1}^{n}$ in the limit: $$ \tiny \begin{equation} \lim_{T\rightarrow\infty}\left[\frac{1}{n}\sum_{i=1}^{n}\mathbb{E}\left\{\gamma^\top\hat{\Sigma}_{i}\gamma-\exp(\bx_{i}^\top \beta)\right\}^{2}-\frac{1}{n}\sum_{i=1}^{n}\mathbb{E}\left\{\gamma^\top S_{i}^{*}\gamma-\exp(\bx_{i}^\top \beta)\right\}^{2}\right]=0 \end{equation} $$ $$ \scriptsize \begin{equation} \Leftrightarrow \quad \mathbb{E}\|\hat{\Sigma}_{i}- S_{i}^{*}\|^{2} \rightarrow 0, \quad \text{for } i=1,\dots,n. \end{equation} $$

Our Covariate-dependent Shrinkage CAP (CS-CAP) is optimal

Simu: new CS-CAP vs L-W and CAP

Analysis of ADNI Data

  • The Alzheimer’s Disease Neuroimaging Initiative (ADNI): launched in 2003, for studying ADRD
  • Alzheimer's Disease Related Dementias (ADRD) affects more than 6 million US people, and 55 million worldwide
  • No known* treatment to stop or prevent ADRD
  • fMRI and brain connectivity likely to be interrupted prior to dementia
  • APOE-$\varepsilon$4 gene, strong risk factor and potential treatment target

Covariate Implicated Components


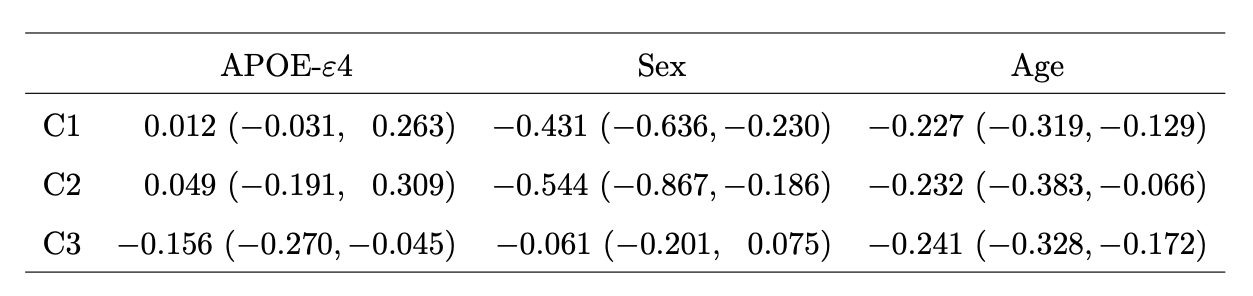
  • First two components related to age and sex
  • Last C3 predicted by age and APOE-$\varepsilon$4 gene

C3: APOE Areas Found by CS-CAP


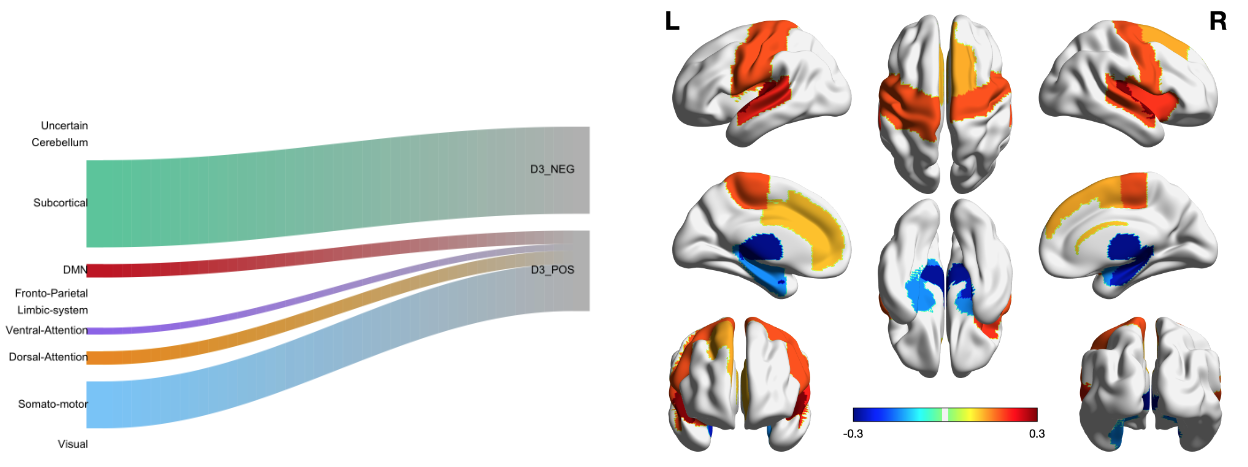
Groups of regions with more or less connections predicted by APOE-$\varepsilon$4 (non)-carriers

Discussion

Thank you!


Comments? Questions?




BigComplexData.com

or BrainDataScience.com