Network Communities and Variable Clustering via CORD
Xi (Rossi) Luo
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science
The ABCD Research Group

June 7, 2016
Funding: NSF/DMS (BD2K) 1557467; NIH P20GM103645, P01AA019072, P30AI042853; AHA
Collaborators

Florentina Bunea
Cornell University

Christophe Giraud
Paris Sud University
Data Science Problem
- We are interested in
big cov with many variablesGlobal property for certainjoint distributions- Real-world cov: maybe
non-sparse and other structures
- Clustering successful for > 40 years and for DSDonoho, 2015
- Exploratory Data Analysis (EDA)Tukey, 1977
- Hierarchical clustering and KmeansHartigan & Wong, 1979
- Usually based on
marginal/pairwise distances
- Can clustering and big cov estimation be combined?
Example: SP 100 Data
- Daily returns from stocks in SP 100
- Stocks listed in Standard & Poor 100 Indexas of March 21, 2014
- between January 1, 2006 to December 31, 2008
- Each stock is a variable
- Cov/Cor matrices (Pearson's or Kendall's tau)
-
Re-order stocks by clusters - Compare cov patterns with different clustering/ordering
-
Cor after Grouping by Clusters
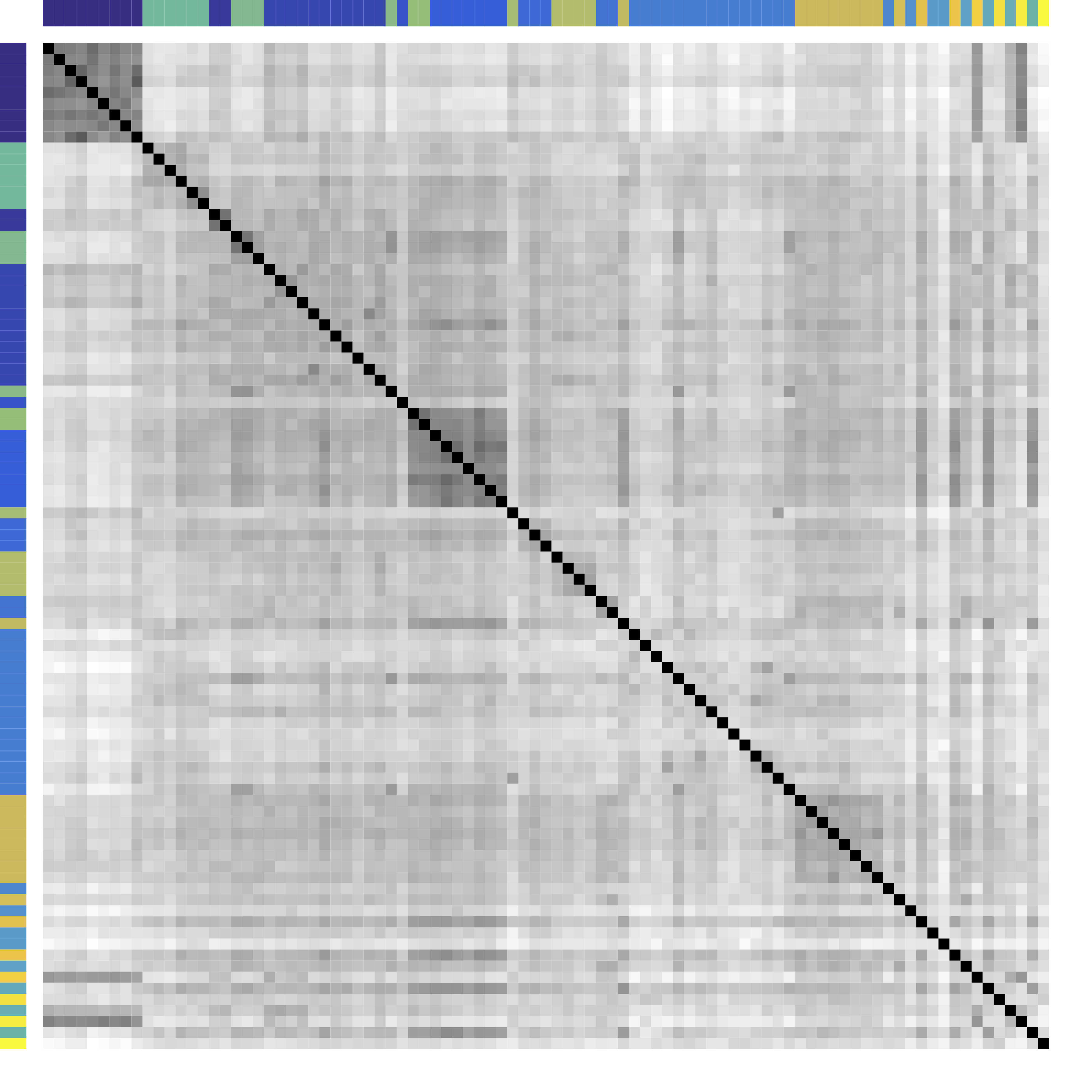

Ours yields stronger
Color bars: variable groups/clusters
Off-diagonal: correlations across clusters
Clustering Results
| Industry |
|
Kmeans | Hierarchical Clustering |
|---|---|---|---|
| Telecom | ATT, Verizon | ATT, Verizon, Pfizer, Merck, Lilly, Bristol-Myers | ATT, Verizon |
| Railroads | Norfolk Southern, Union Pacific | Norfolk Southern, Union Pacific | Norfolk Southern, Union Pacific, Du Pont, Dow, Monsanto |
| Home Improvement | Home Depot, Lowe’s | Home Depot, Lowe’s, Starbucks | Home Depot, Lowe’s, Starbucks, Costco, Target, Wal-Mart, FedEx, United Parcel Service |
| $\cdots$ | |||
Model
Problem
- Let ${X} \in \real^p$ be a zero mean random vector
- Divide variables into partitions/clusters
- Example: $\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$
- Theoretical: Find a partition $G = \{G_k\}_{ 1 \leq k \leq K}$ of $\{1, \ldots, p\}$ such that all $X_a$ with $a \in G_k$ are
"similar" - DS: find a
"helpful" partition that show patterns
Related Methods
- Clustering: Kmeans and hierarchical clustering
- Advantages: fast, general, popular
- Limitations: low signal-noise-ratio, theory
- Community detection: huge literature see review Newman, 2003 but start with observed
adjacency matrices
Kmeans
Low noise
High noise
- Cluster points together if pairwise distance small
- Clustering accuracy
depends on the noise
Kmeans: Generative Model
- Data $X_{n\times p}$: $p$ variables from partition $G$: $$G=\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$$
- Mixture Gaussian: if variable $X_j \in \real^n$ comes from cluster $G_k$ Hartigan, 1975 $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j $$
- Kmeans minimizes over $G$ (and centroid $Z$): $$\sum_{k=1}^K \sum_{j\in G_k} \left\| X_j - Z_k \right\|_2^2 $$
$G$-Latent Cov
- We call $G$-latent model: $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j \mbox{ and } j\in G_k $$
- WLOG, all variables are standardized
- Intuition: variables $j\in G_k$ form net communitiesLuo, 2014
Model
$$ X_{n\times p}=\underbrace{Z_{n\times k}}_\text{Source/Factor} \quad \underbrace{G_{k\times p}}_\text{Mixing/Loading} + \underbrace{E_{n\times p}}_{Error} \qquad Z \bot E$$
- Clustering: $G$ is $0/1$ matrix for $k$ clusters/ROIs
- Decomposition:
- PCA/factor analysis: orthogonality
- ICA: orthogonality → independence
- matrix decomposition: e.g. non-negativity
- Observing $X$, we show identifiability for non-diag or even
"negative" $\cov(Z)$ - Can generalize to semiparametric distributions
Principals in Other Clustering
- The Euclidean distance for hierarchical clustering and Kmeans, for two columns/voxles $X_a$ and $X_b$: $$ \|X_a - X_b \|_2^2 = 2(1-\cor(X_a, X_b)) $$
- Recall $X_i = Z_k + E_i$ $i \in G_k$; cor depends on $\var(E)$
- Even worse, if $\var(E)$ or SNRs vary across clusters, the distance between $X_a$ and $X_b$ is
- larger even if generated by same $Z$ and large error
- smaller even if generated by different $Z$ and small error
Generalization
Example: $G$-Block
-
Set $G=\ac{\ac{1,2};\ac{3,4,5}}$, $X \in \real^p$ has $G$-block cov
$$\Sigma =\left(\begin{array}{ccccc} {\color{red} D_1} & {\color{red} C_{11} }&C_{12} & C_{12}& C_{12}\\ {\color{red} C_{11} }&{\color{red} D_1 }& C_{12} & C_{12}& C_{12} \\ C_{12} & C_{12} &{\color{green} D_{2}} & {\color{green} C_{22}}& {\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} D_2}&{\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} C_{22}}&{\color{green} D_2} \end{array}\right) $$ - Matrix math: $\Sigma = G^TCG + d$
- We allow $|C_{11} | \lt | C_{12} |$ or $C \prec 0$
- Kmeans/HC leads to block-diagonal cor matrices (permutation)
- Clustering based on $G$-Block, generalizing $G$-Latent which requires $C\succ 0$
Defining Order of Partitions
- $G\leq G^{\prime}$ if $G^{\prime}$ is a sub-partition of $G$
- Example: $G^{\prime} =\{\{1\}, \{2\}, \{3\}\}$, $G=\{1,2,3\}$
- Denote $a\stackrel{G(X)}{\sim} b$ by the partition $G(X)$ if $\var(X_{a})=\var(X_{b})$ and $\cov(X_{a},X_{c})=\cov(X_{b},X_{c})$ for all $c\neq a,b$
- Note that $a\stackrel{G^{\prime}(X)}{\sim} b$ if $G\leq G^{\prime}$
- Exist multiple partitions that yield $G$-block cov
Minimum $G$ Partition
The minimal partition is unique under regularity conditions.
Method
New Metric: CORD
- First, pairwise correlation distance (like Kmeans)
- Gaussian copula: $$Y:=(h_1(X_1),\dotsc,h_p(X_p)) \sim N(0,R)$$
- Let $R$ be the correlation matrix
- Gaussian: Pearson's
- Gaussian copula: Kendall's tau transformed, $R_{ab} = \sin (\frac{\pi}{2}\tau_{ab})$
Algorithm: Main Idea
- Greedy: one cluster at a time, avoiding NP-hard
- Cluster variables together if CORD metric $$\widehat \d(a,b) \lt \alpha$$ where $\alpha$ is a tuning parameter
- $\alpha$ is chosen by theory or CV
Theory
Condition
The signal strength $\eta$ is large.
Consistency
Ours recovers the exact clustering with high probability.
Minimax
Group separation condition on $\eta$ is necessary.
Simulations
Setup
- Generate from various $C$: block, sparse, negative
- Compare:
- Exact recovery of groups (theoretical tuning parameter)
- Cross validation (data-driven tuning parameter)
- Cord metric vs (semi)parametetric cor (regardless of tuning)
Exact Recovery
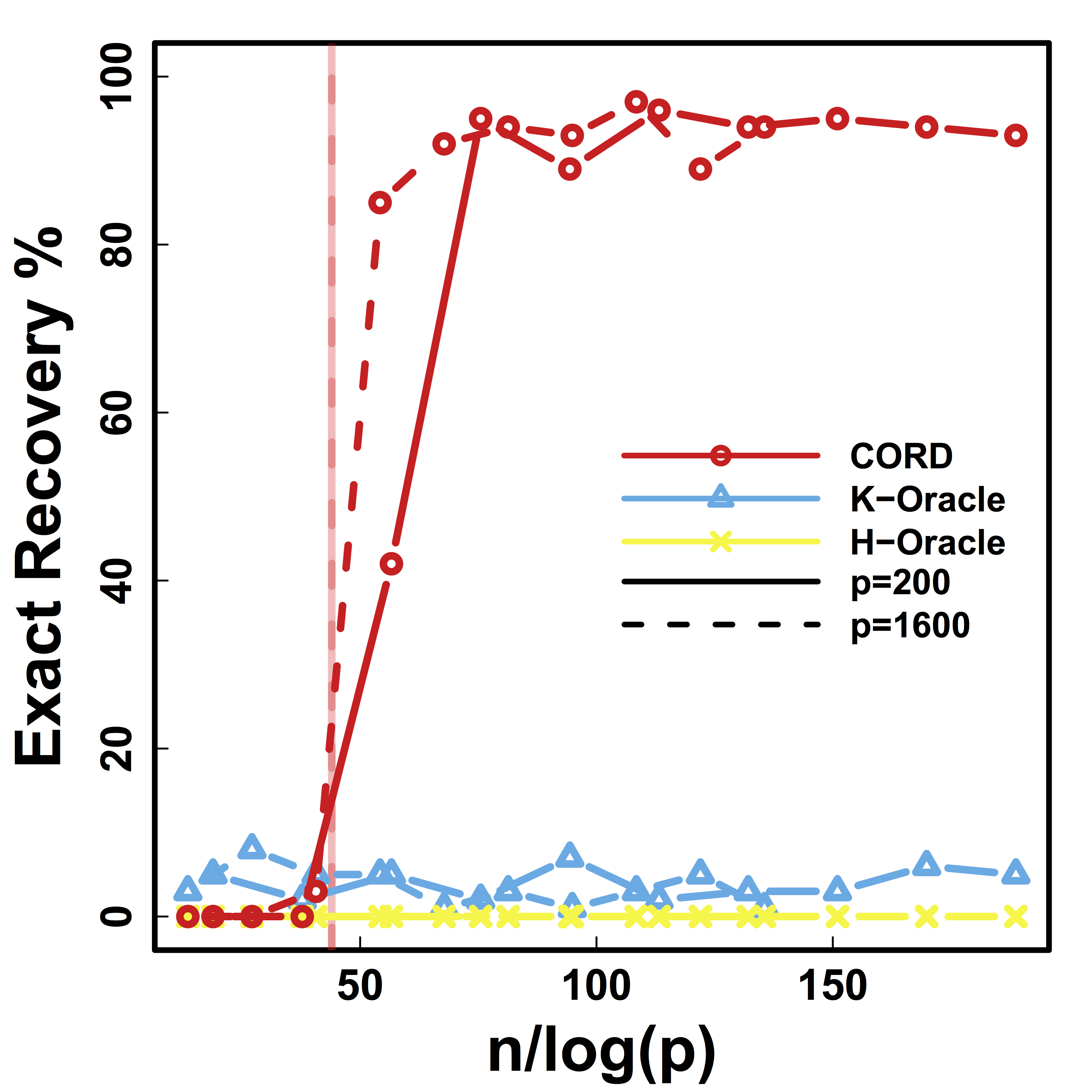
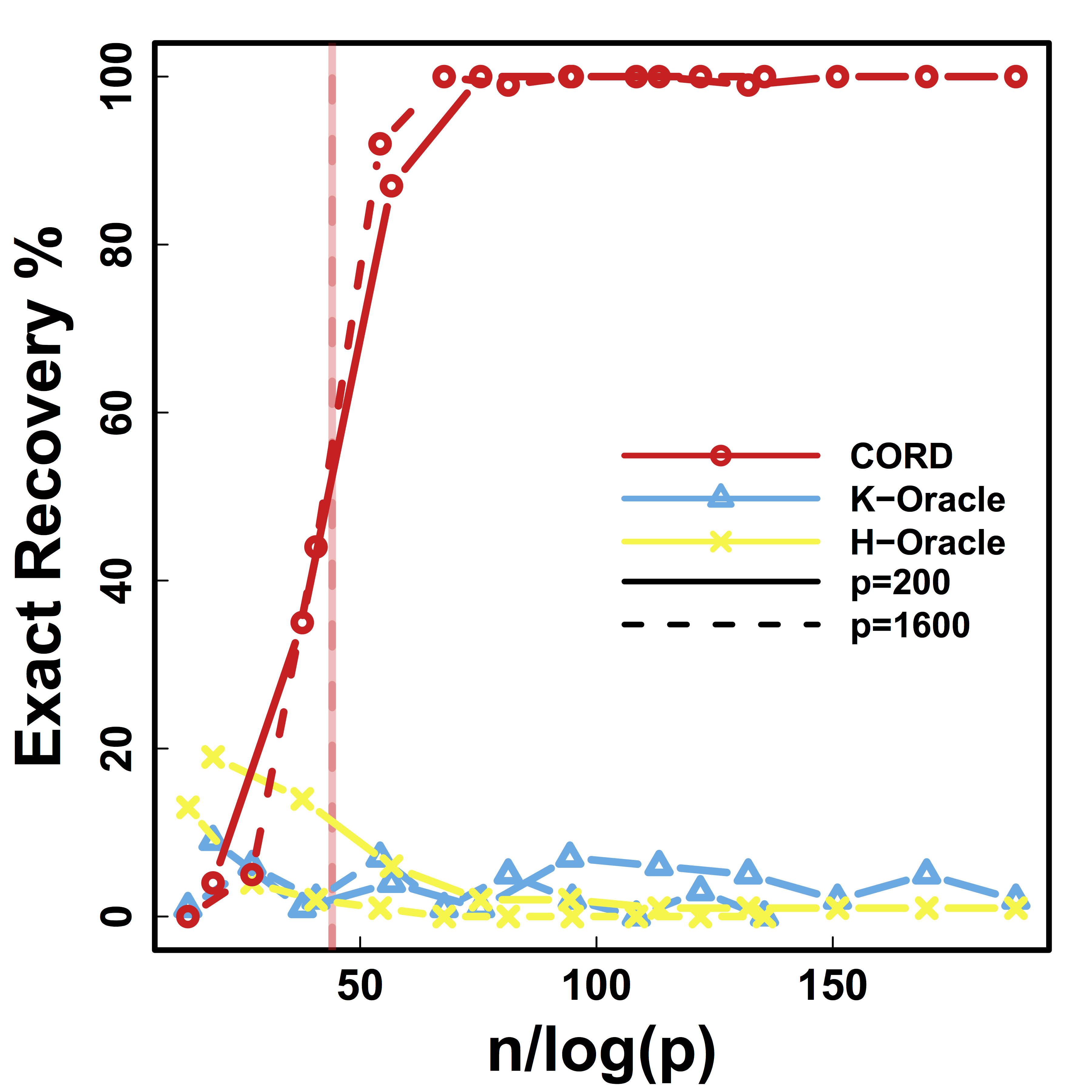
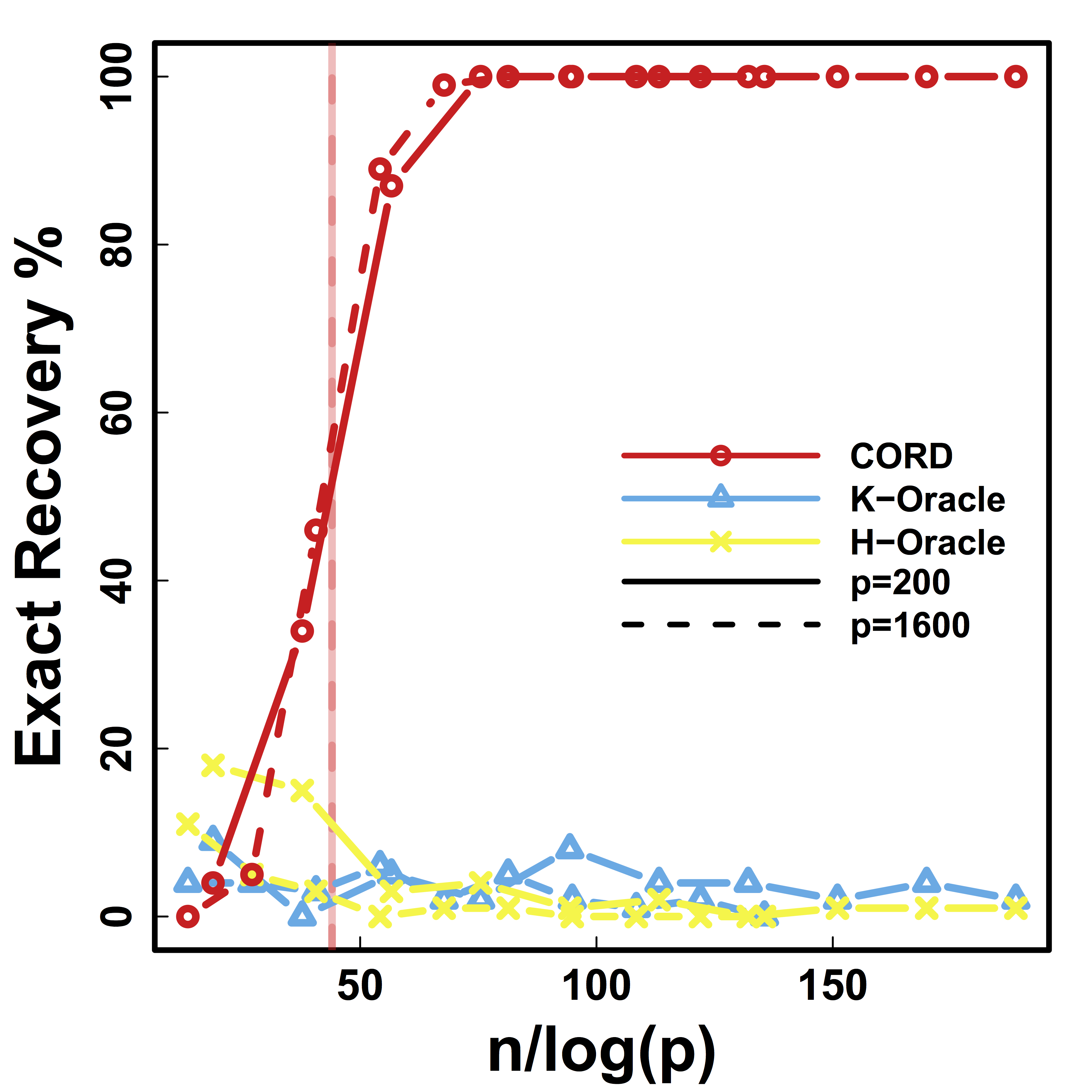
Different models for $C$="$\cov(Z)$" and $\alpha = 2 n^{-1/2} \log^{1/2} p$
Vertical lines: theoretical sample size based on our lower bound
HC and Kmeans fail even if inputting the true $K$.
Data-driven choice of $\alpha$
- Given $G$ and $R$, we introduce a block averaging operator $\left[\varUpsilon\left(R,G\right)\right]_{ab} =$
$$\begin{cases} \left|G_{k}\right|^{-1}\left(\left|G_{k}\right|-1\right)^{-1}\sum_{i,j\in G_{k},i\ne j}R_{ij} & \mbox{if } a\ne b \mbox{ and } k=k^{\prime}\\ \left|G_{k}\right|^{-1}\left|G_{k^{\prime}}\right|^{-1}\sum_{i\in G_{k},j\in G_{k^{\prime}}}R_{ij} & \mbox{if } a\ne b \mbox{ and } k\ne k^{\prime}\\ 1 & \mbox{if }a=b. \end{cases} $$ - We choose $\alpha$ via cross validation using minimization over a grid of $\alpha$: $$\min_\alpha \| \varUpsilon\left(\hat R,G_\alpha \right) - \hat{R}_{test}\|_F^2 $$
Cross Validation
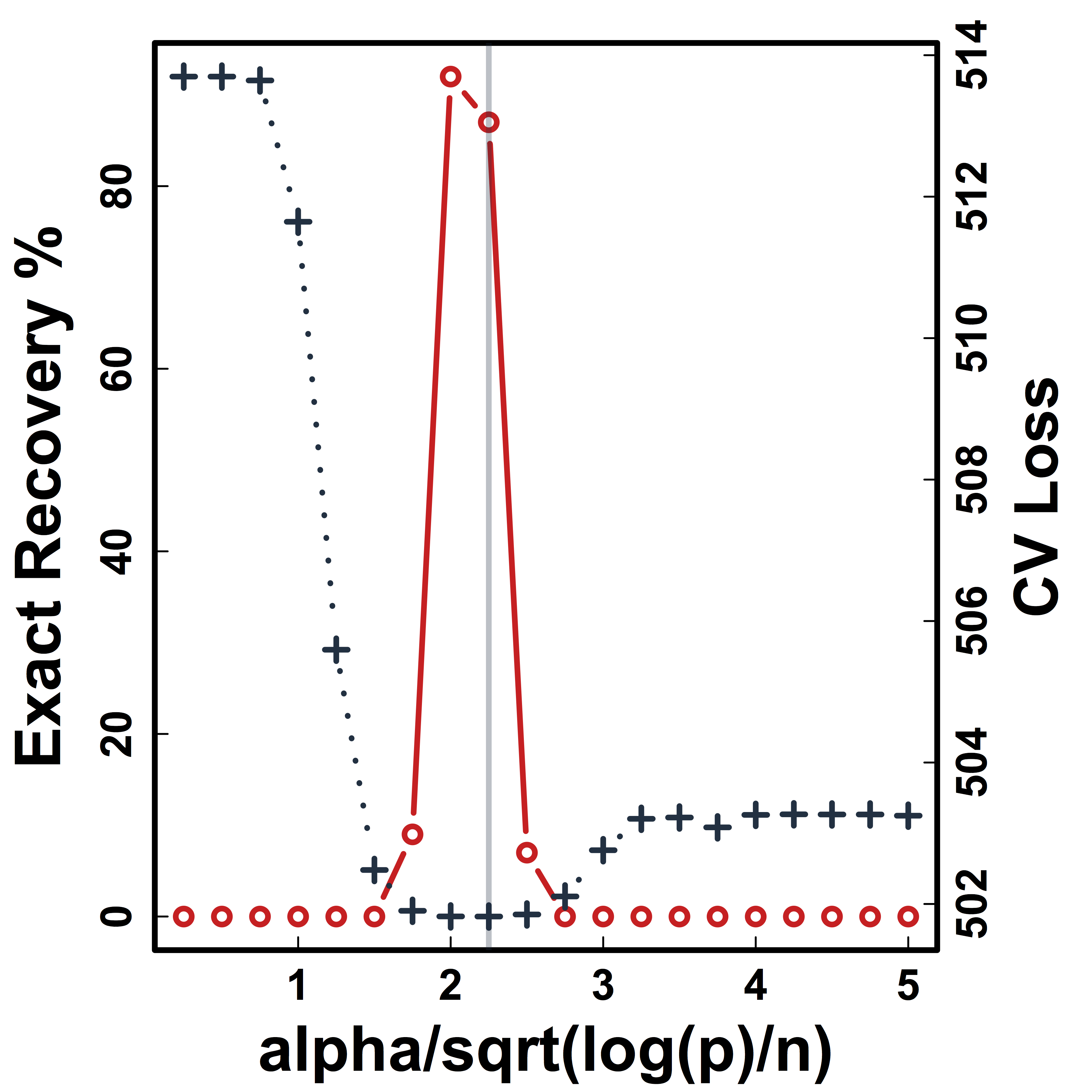
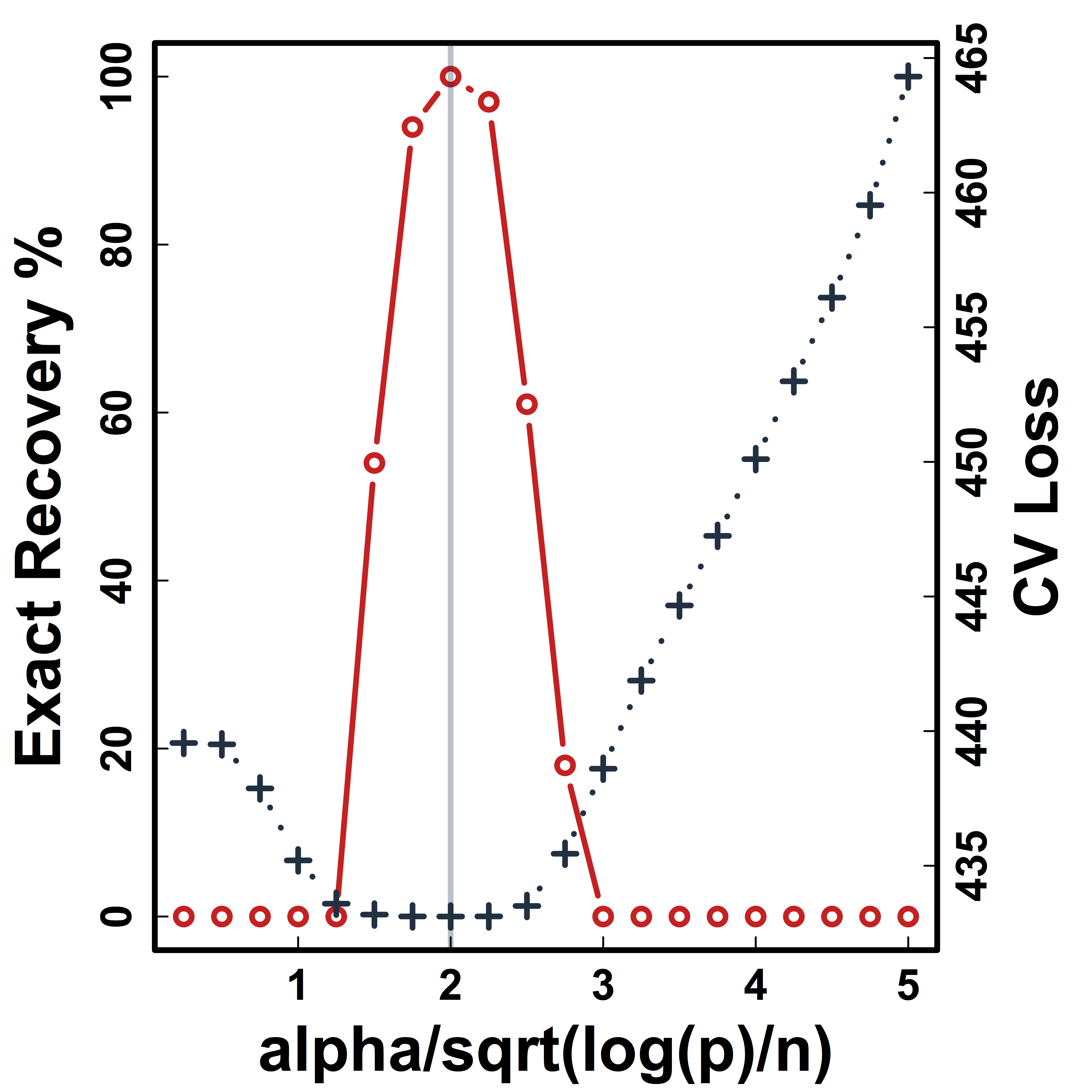
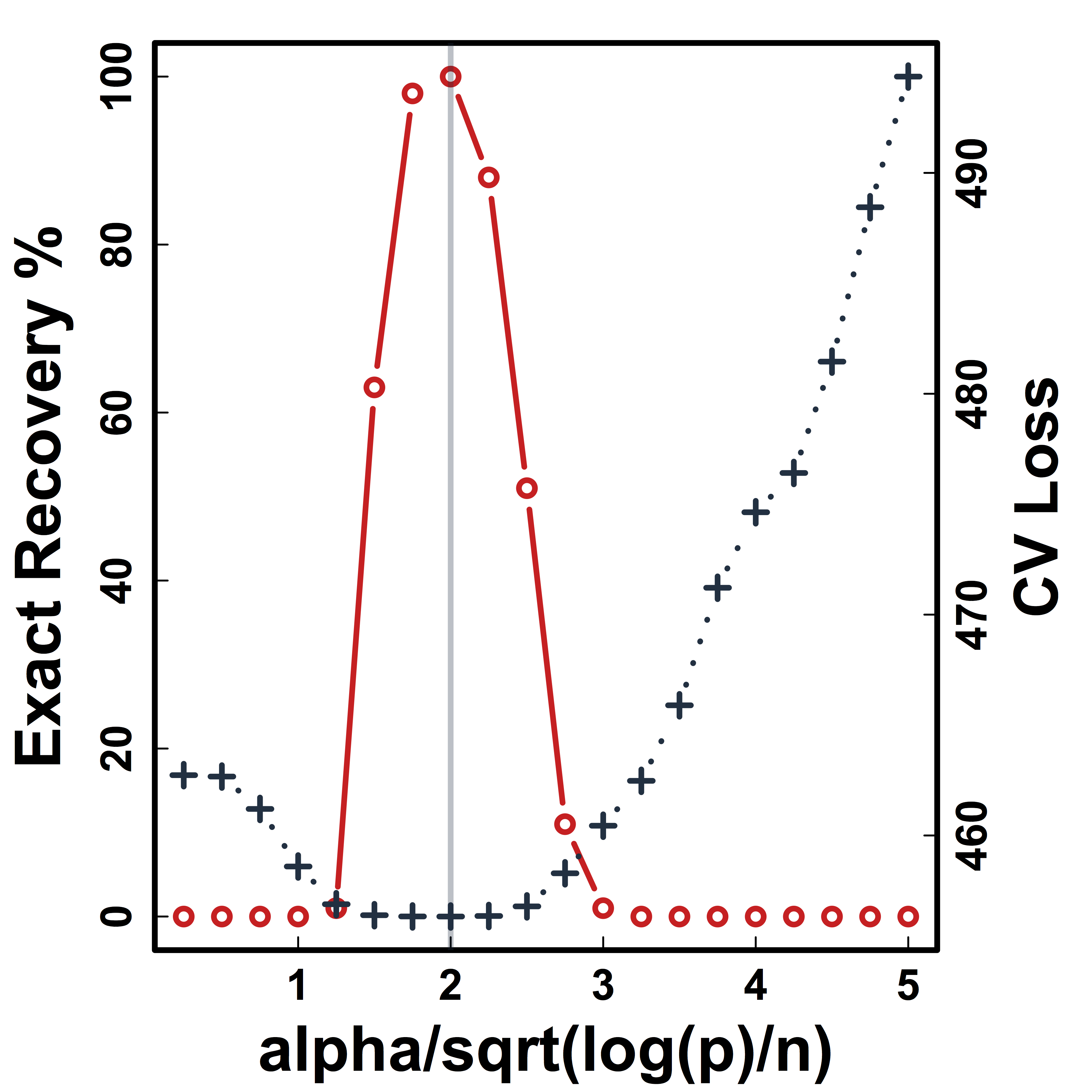
Recovery % in red and CV loss in black.
CV selects the constants to yield close to 100% recovery.
Metric Comparison: Without Threhold
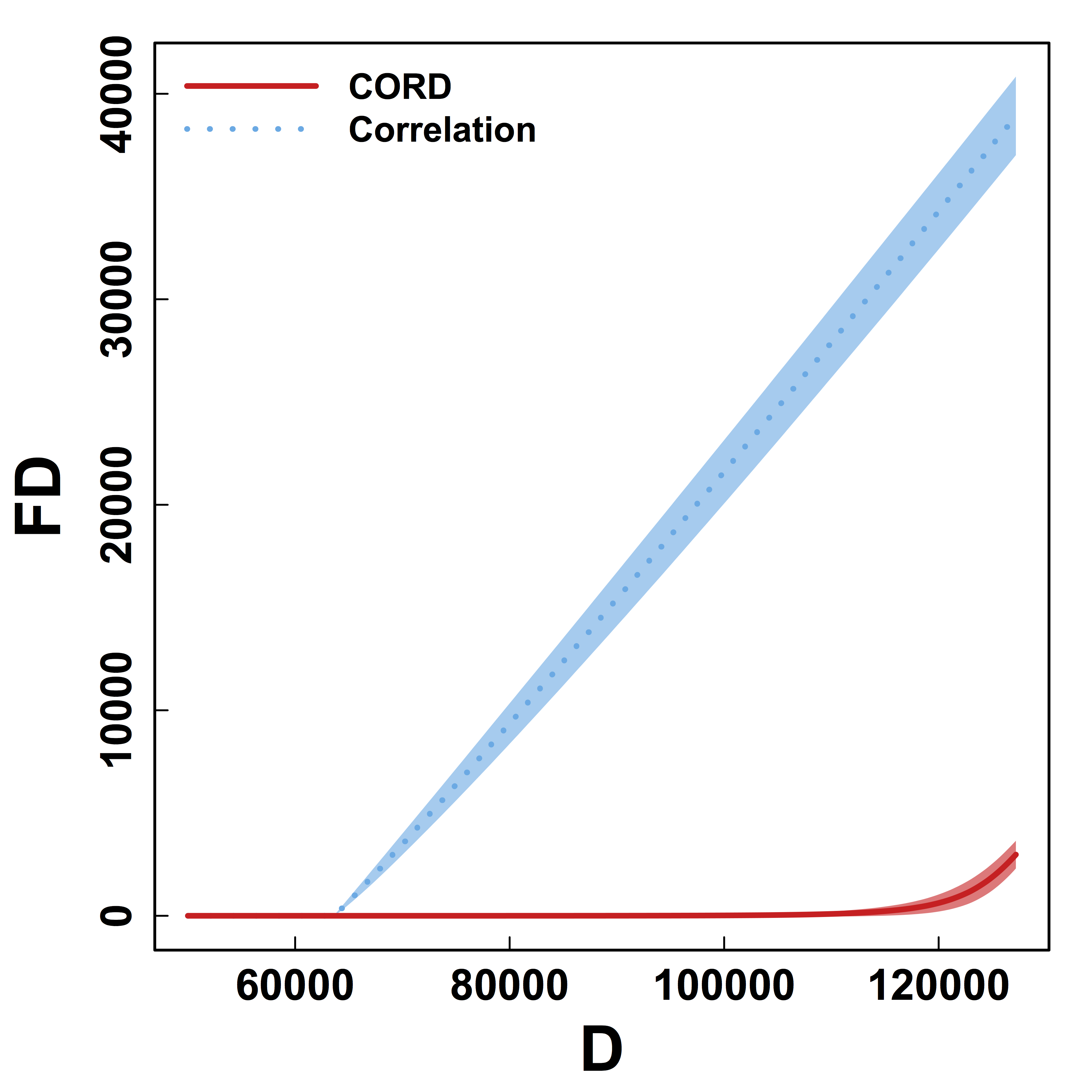
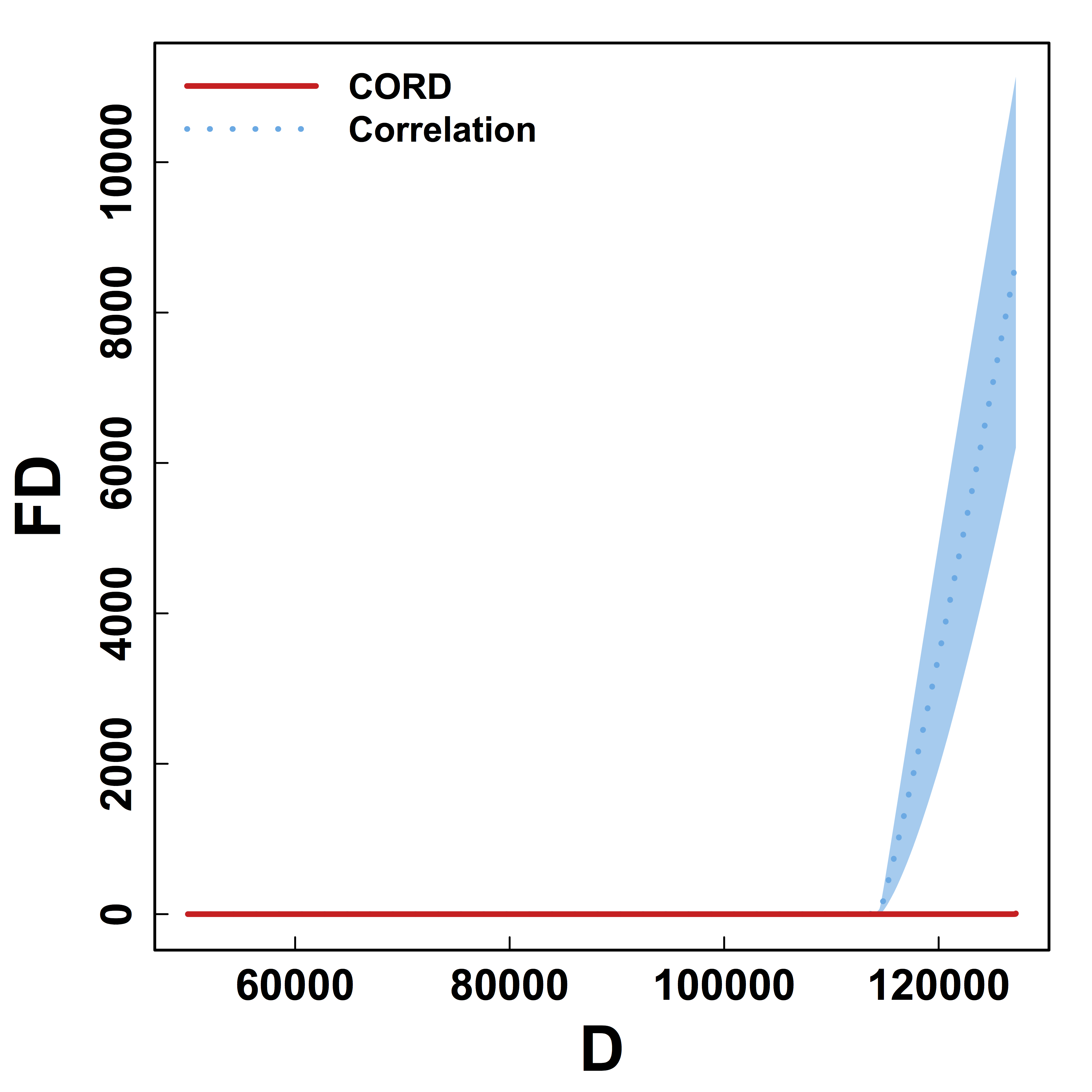
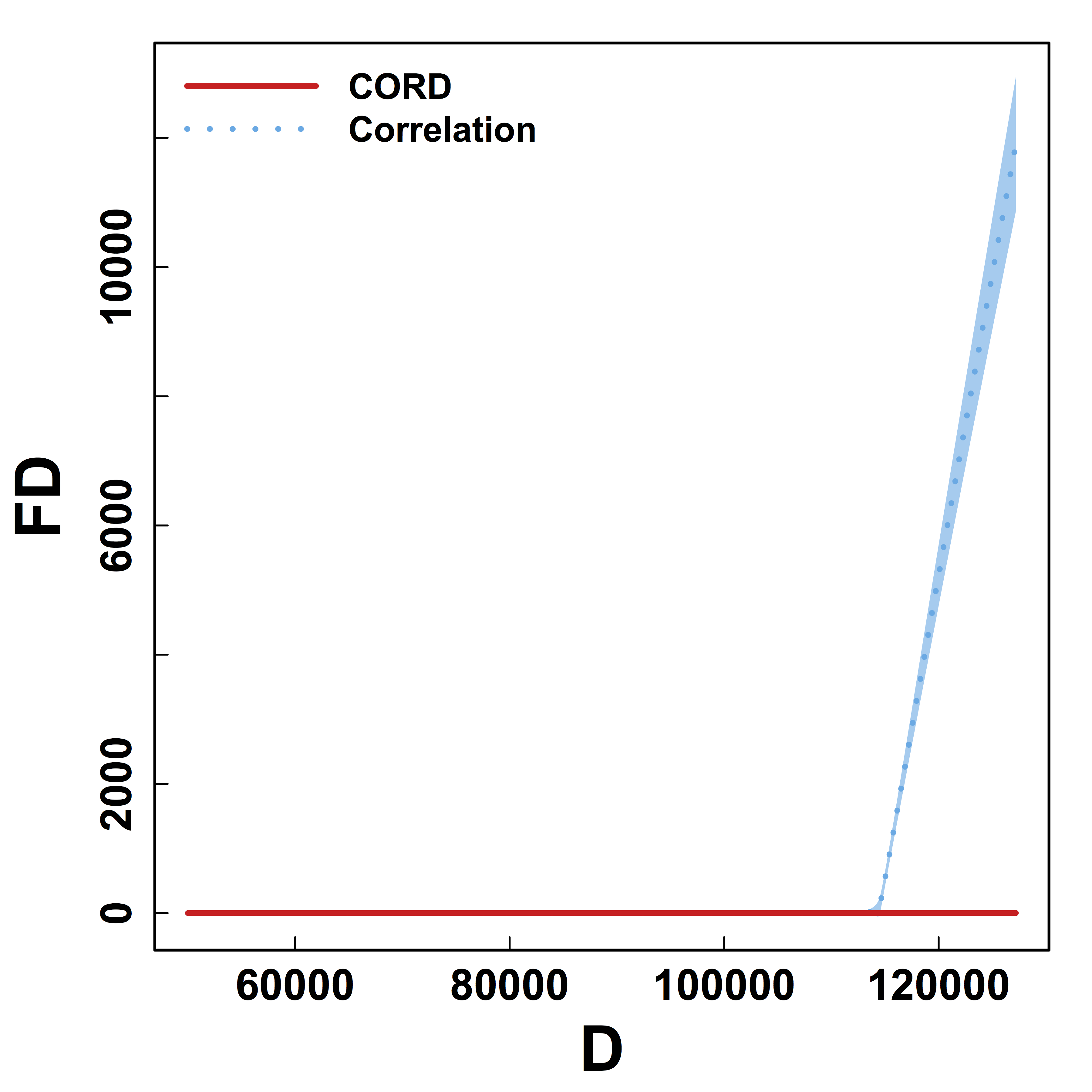
HC and Kmeans metrics yield more false discoveries (FD) as the threshold (or $K$) varies.
Better metric for clustering regardless of threshold.
Real Data
fMRI data: blood-oxygen-level dependent (BOLD) signals from each
fMRI Studies
Sub 1, Sess 1

Time 1

2
…

~200
⋮
Sub i, Sess j


…

⋮
Sub ~100, Sess ~4


…

This talk: one subject, two sessions (to test replicability)
Functional MRI
- fMRI matrix: BOLD from different brain regions
- Variable: different brain regions
- Sample: time series (after whitening or removing temporal correlations)
-
Clusters of brain regions
- Two data matrices from two scan sessions OpenfMRI.org
- Use Power's 264 regions/nodes
Test Prediction/Reproducibilty
- Find partitions using the first session data
- Average each block cor to improve estimation
- Compare with the cor matrix from the second scan $$ \| Avg_{\hat{G}}(\hat{\Sigma}_1) - \hat{\Sigma}_2 \|$$
- Difference is smaller if clustering $\hat{G}$ is better
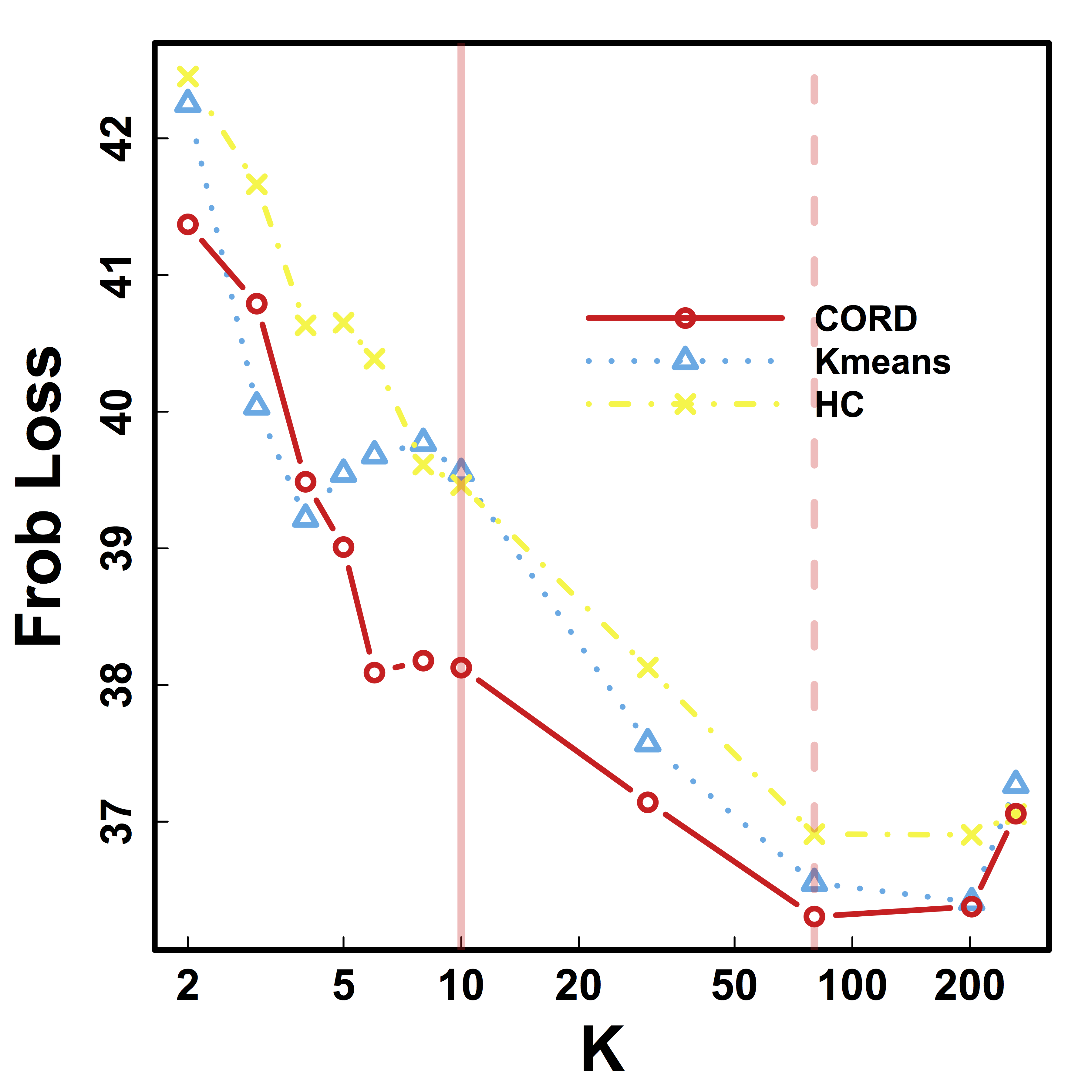
Vertical lines: fixed (solid) and data-driven (dashed) thresholds
Prediction Comparison: smaller prediction loss for almost all $K$
Discussion
- Cov + clustering:
- Identifiability, accuracy, optimality
- $G$-models: $G$-latent, $G$-block, $G$-exchangeable
- New metric, method, and theory
- Paper: google
"cord clustering" (arXiv 1508.01939) - R package:
cord on CRAN
Thank you!
Slides at: bit.ly/SLDS16
