Estimating Causal Pathway Effects via Large-scale Multilevel Models
Xi (Rossi) Luo
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science

May 4, 2016
Funding: NSF/DMS (BD2K) 1557467; NIH P20GM103645, P01AA019072, P30AI042853; AHA
Coauthor

Yi Zhao
(3rd Yr PhD Student)
Brown University
Stop/Go Task fMRI
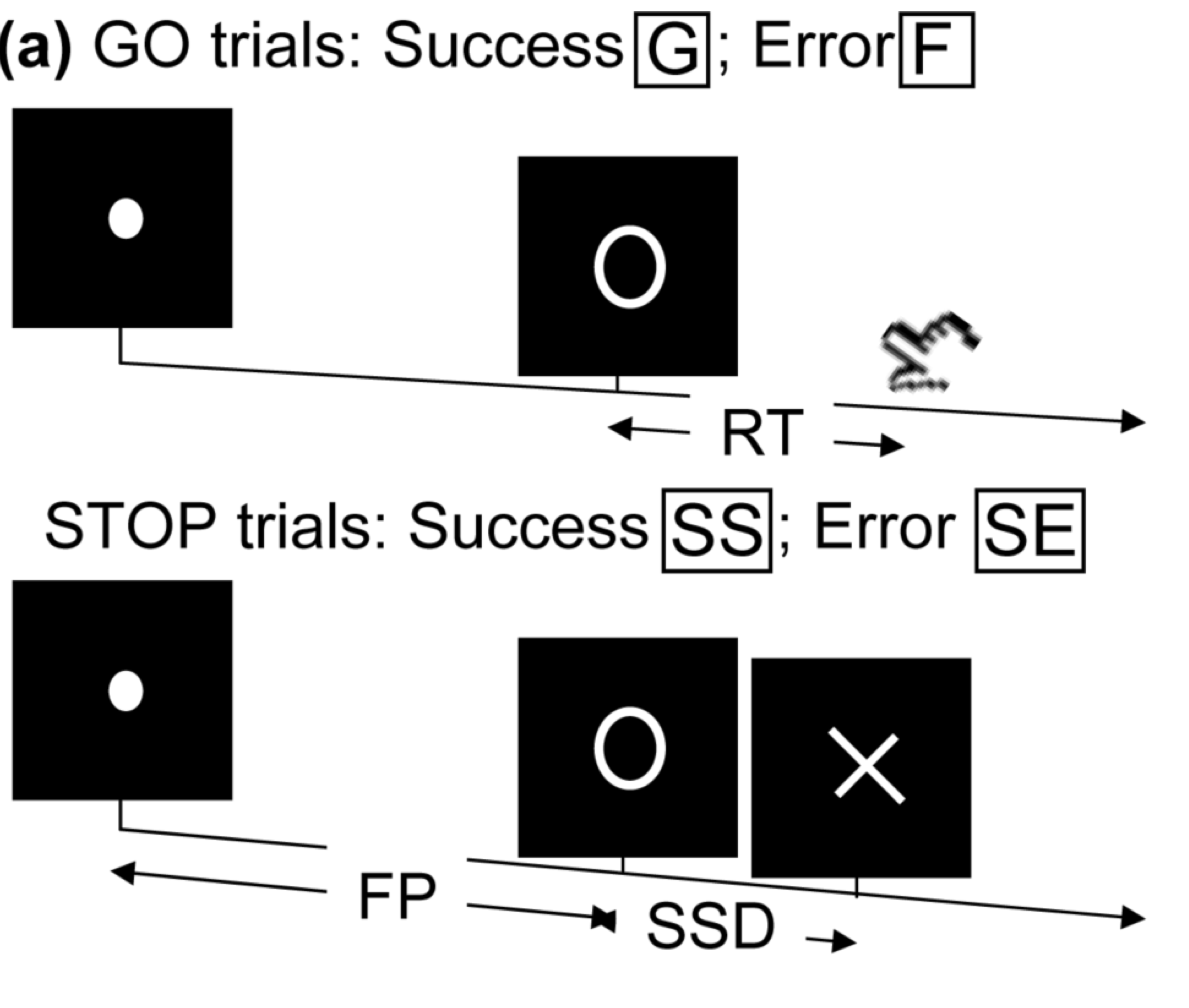
- Task fMRI: performs tasks under brain scanning
-
Randomized stop/go task:- press button if "go";
- withhold pressing if "stop"
- Not resting-state: "rest" in scanner
fMRI data: blood-oxygen-level dependent (BOLD) signals from each
Raw Data: Motor Region
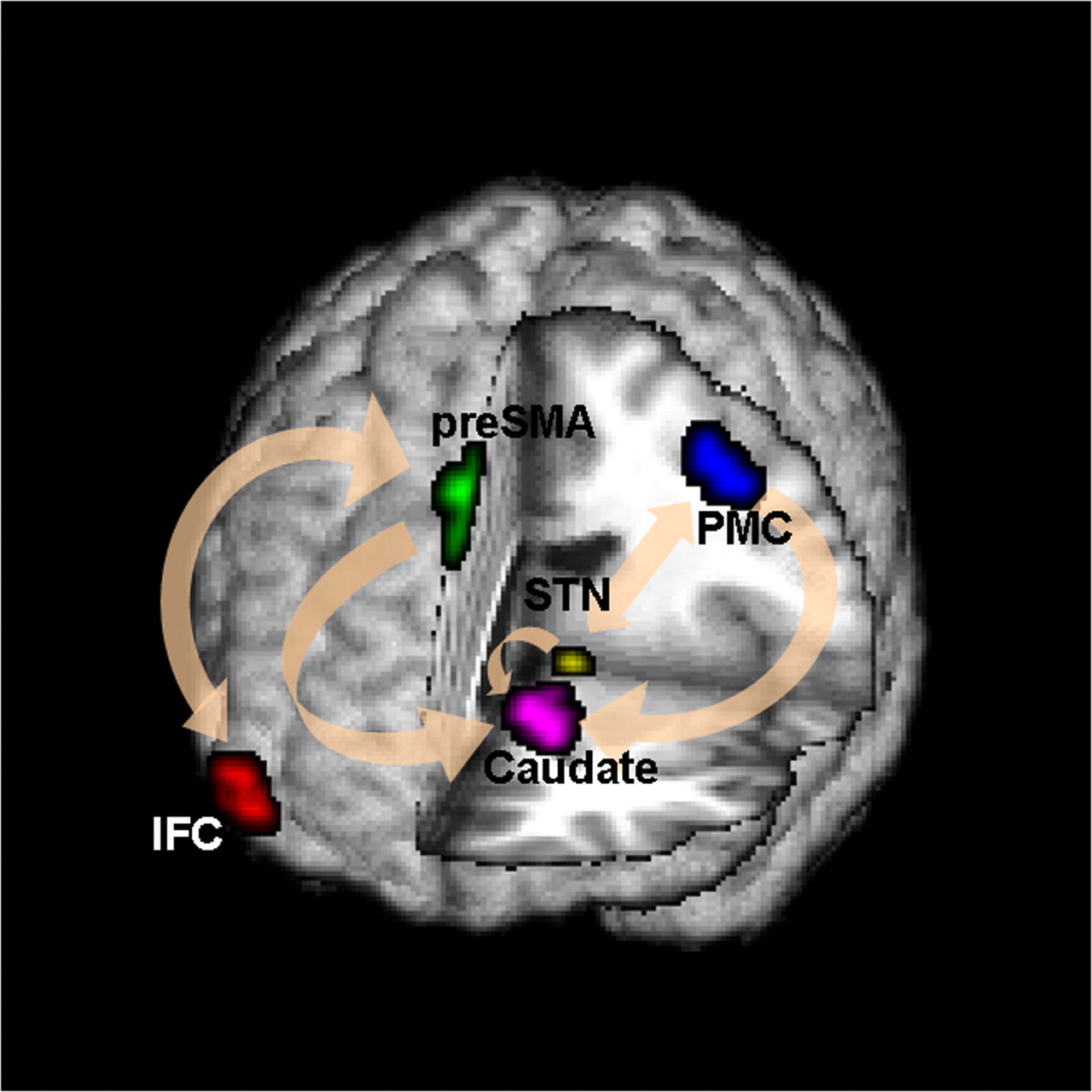
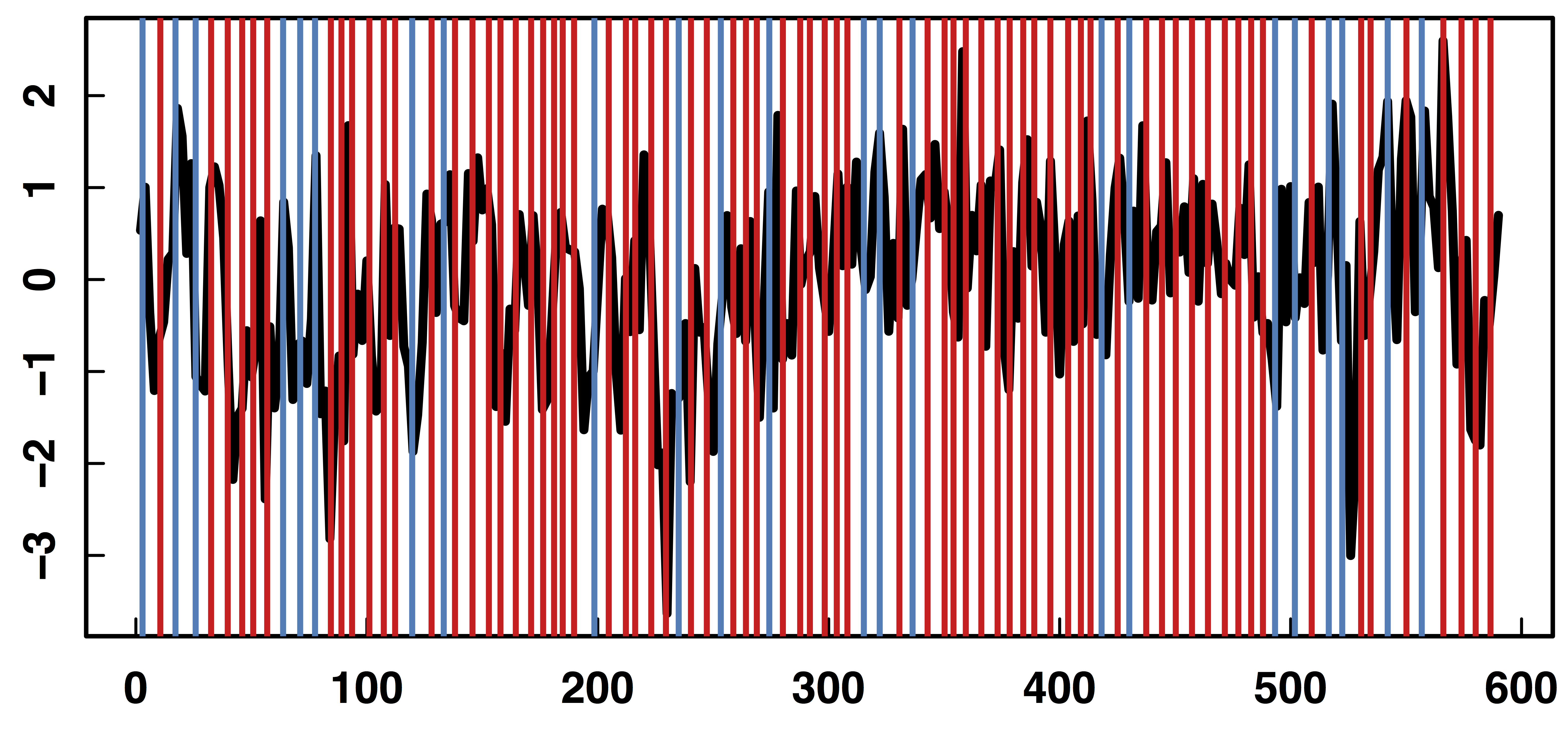
fMRI Studies
Sub 1, Sess 1

Time 1

2
…

~300
⋮
Sub i, Sess j


…

⋮
Sub ~100, Sess ~4


…

Our data: 98 subjects × 4 sessions × 100 trials × 2 regions
Question: can "big and complex" fMRI data be helpful?
Brain Networks
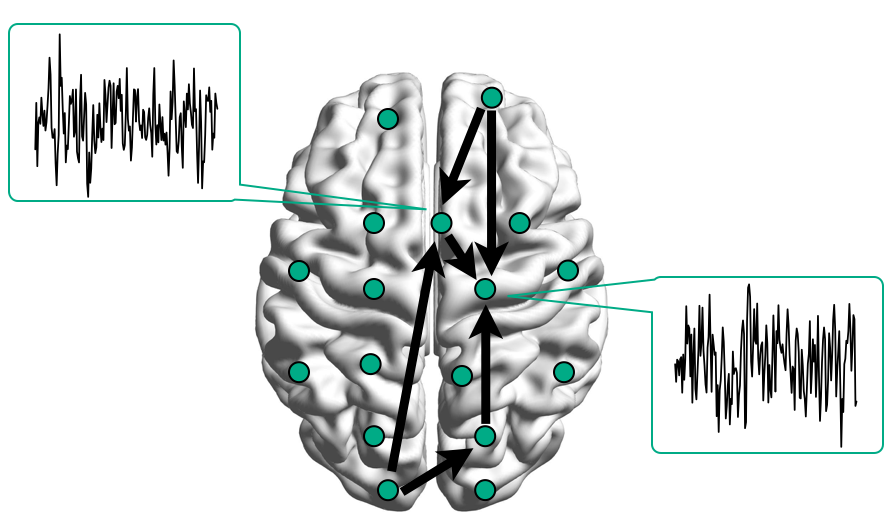
Functional/Effective Connectivity
Network Model with Stimulus
Goal: quantify effects stimuli → preSMA → PMC regions Duann, Ide, Luo, Li (2009). J of Neurosci
Model
Mediation Analysis and SEM
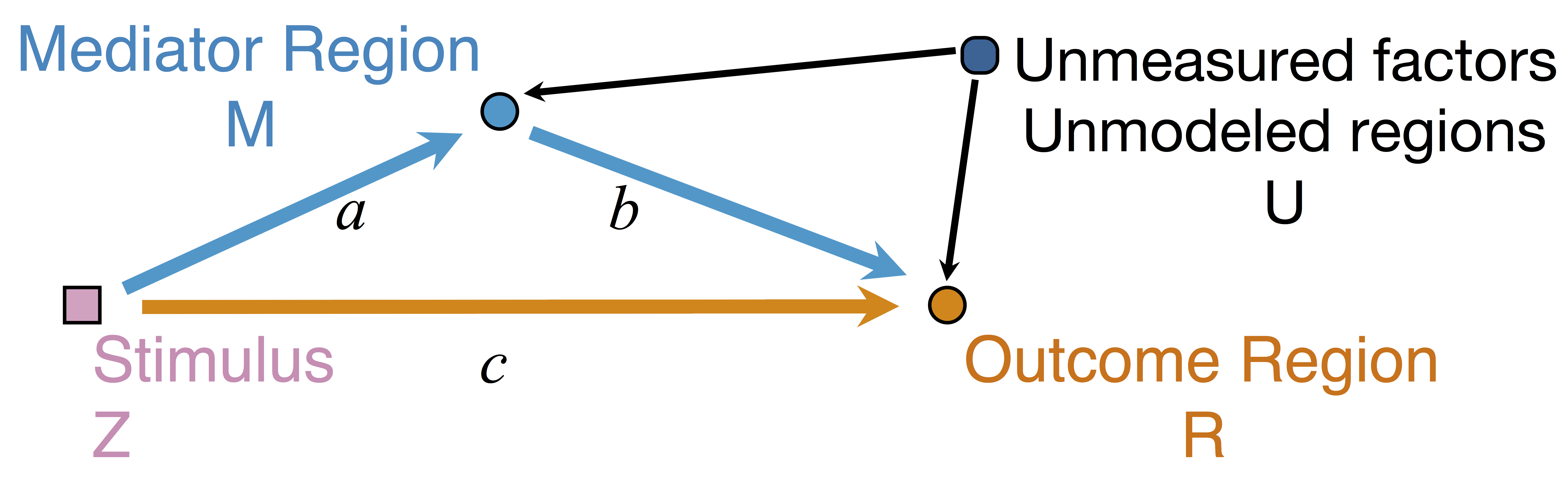 $$\begin{align*}M &= Z a + \overbrace{U + \epsilon_1}^{E_1}\\ R &= Z c + M b + \underbrace{U g + \epsilon_2}_{E_2}, \quad \epsilon_1 \bot \epsilon_2\end{align*}$$
$$\begin{align*}M &= Z a + \overbrace{U + \epsilon_1}^{E_1}\\ R &= Z c + M b + \underbrace{U g + \epsilon_2}_{E_2}, \quad \epsilon_1 \bot \epsilon_2\end{align*}$$
-
Indirect effect: $a \times b$; Direct effect: $c$ - Correlated errors: $\delta = \cor(E_1, E_2) \ne 0$ if $U\ne 0$
Mediation Analysis in fMRI
- Mediation analysis (usually assuming $U=0$)
- Baron&Kenny, 86; Sobel, 82; Holland 88; Preacher&Hayes 08; Imai et al, 10; VanderWeele, 15;...
- Parametric Wager et al, 09 and functional Lindquist, 12 mediation, under (approx.) independent errors
- Stimulus $\rightarrow$ brain $\rightarrow$ user reported ratings, one brain mediator
- Assuming $U=0$ between ratings and brain
- Multiple mediators and multiple pathways
- Dimension reduction by arXiv1511.09354Chen, Crainiceanu, Ogburn, Caffo, Wager, Lindquist, 15
- Pathway Lasso penalization Zhao, Luo, 16
- This talk: causal estimation under $U\ne 0$ (its effect size $\delta \ne 0$) when modeling two brain regions

Existing Approaches for $\delta \ne 0$
- Assuming $\delta=0$
- Assumption "too strong" for most cases Imai et al, 10
- Sensitivity plot: "guessing" $\delta$
- Simplify models: e.g. $c=0$ via instrumental variable
- Adjust if possible Sobel, Lindquist, 14
- Use Bayesian prior or regularization
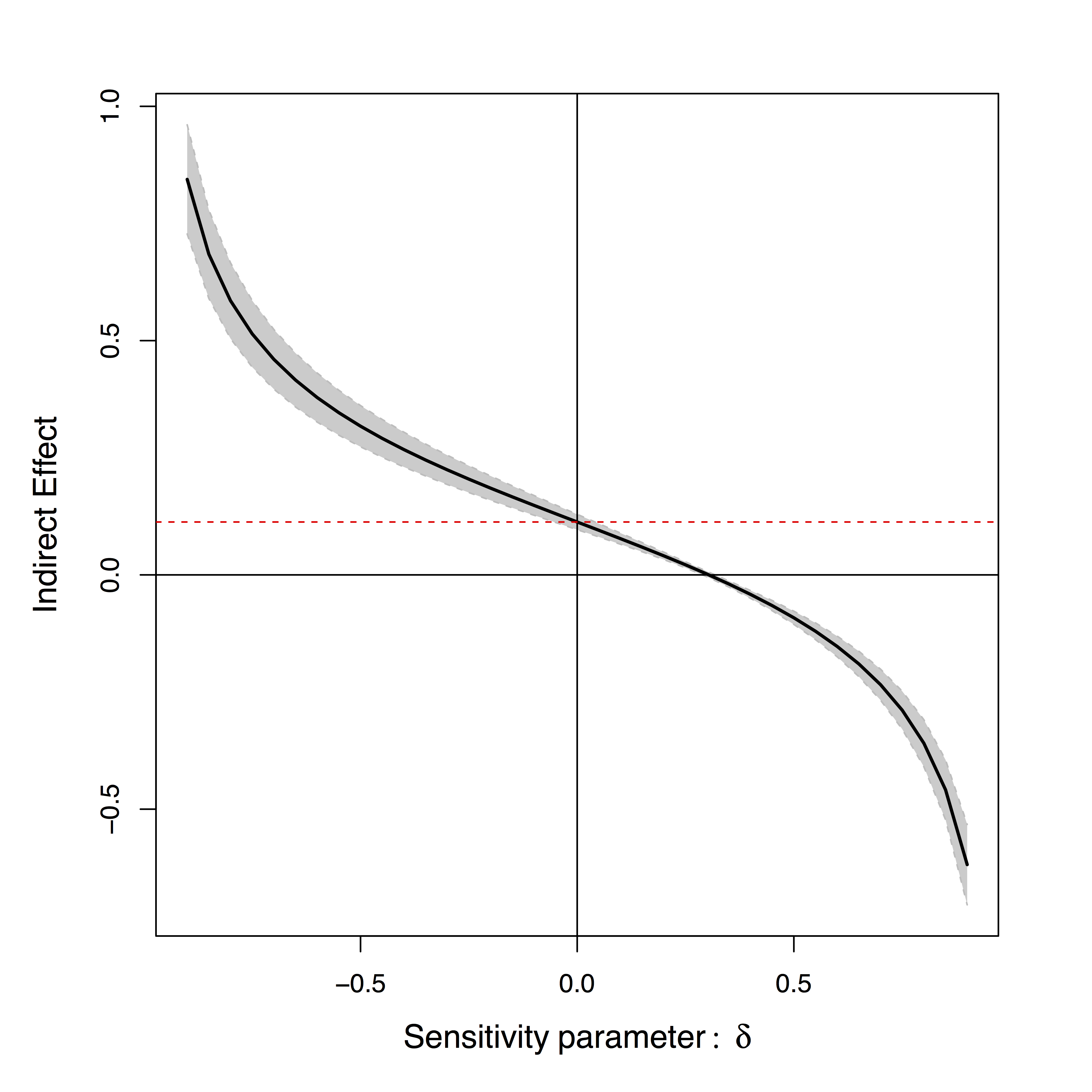
Effects can be positive or negative depending on $\delta$
Method
Our Approach: Step 1
- Bivariate
single-level model $$\begin{align*}\begin{pmatrix}M & R\end{pmatrix} & = \begin{pmatrix}Z & M\end{pmatrix} \begin{pmatrix}a & c\\ 0 & b \end{pmatrix} + \begin{pmatrix}E_{1} & E_{2}\end{pmatrix}\\ (E_1, E_2) & \sim MVN(\boldsymbol{0}, \boldsymbol{\Sigma}) \quad \boldsymbol{\Sigma}=\begin{pmatrix}\sigma_{1}^{2} & \delta\sigma_{1}\sigma_{2}\\ \delta\sigma_{1}\sigma_{2} & \sigma_{2}^{2} \end{pmatrix} \end{align*}$$ - Estimate $(a,b,c,\boldsymbol{\Sigma})$ via ML (a lot of handwaving)
- We solve an optimization with constraints
- Different than running two regressions
Causal Interpretation
- Prove causal using potential outcomes Neyman, 23; Rubin, 74
- Causal inference intuition $$Z \rightarrow \begin{pmatrix} M \\ R \end{pmatrix}$$
- Other approaches assume $$r_{i}\left(z_{i}^{\prime},m_{i}\right)\bot m_{i}\left(z_{i}\right)|Z_{i}=z_{i}$$
- We do not need this assumption
Theory
- Theorem:
Given $\delta$, unique maximizer of likelihood, expressed in closed form - Theorem:
Given $\delta$, our estimator is root-n consistent and efficient - Bias (and variance) depends on $\delta$
Maximum Likelihood: “Tragedy may lurk around a corner”
[Stigler 2007]"Tragedy" of ML
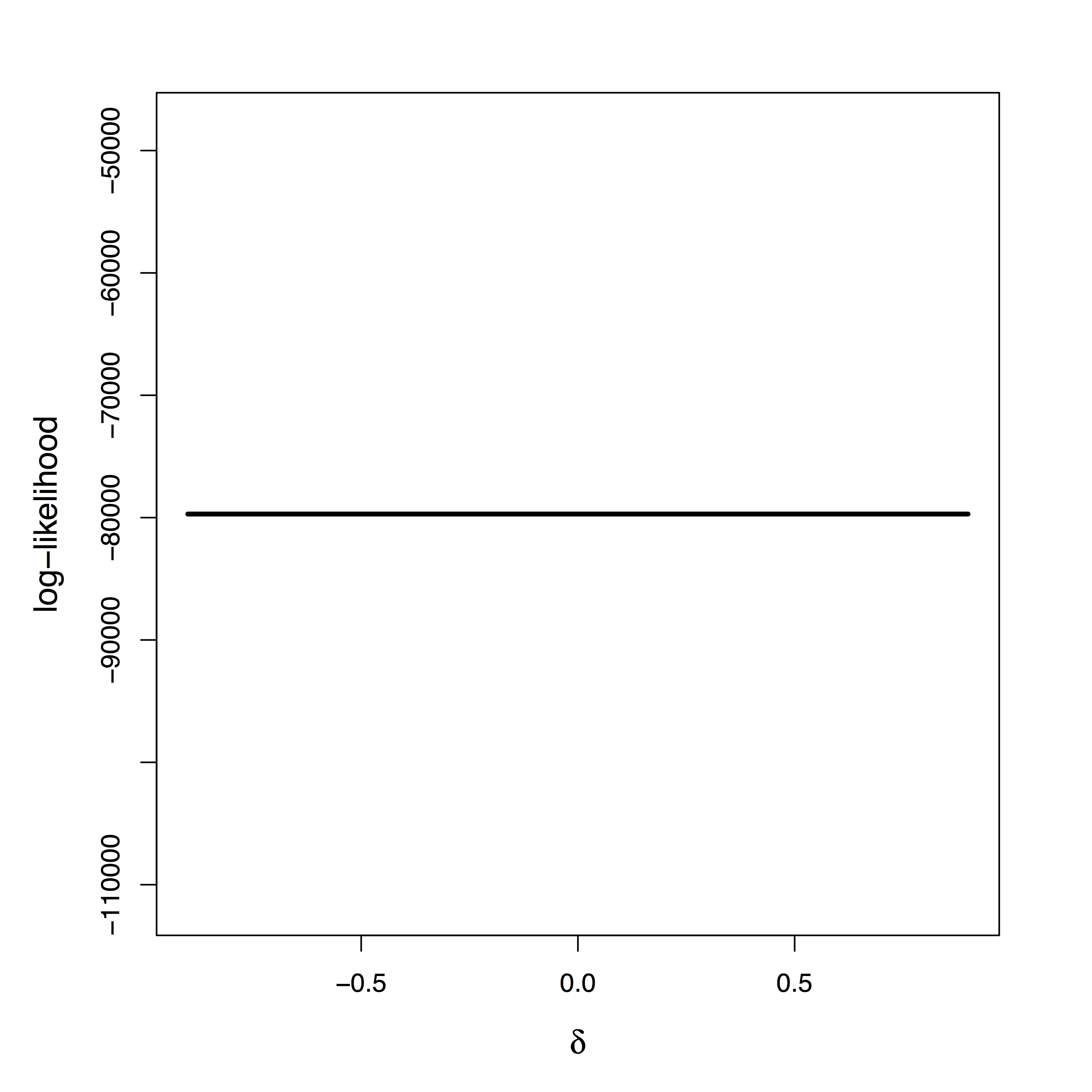
- Likelihood provides
zero info about $\delta$ - Cannot simply use prior on $\delta$
Two different models generate same single-trial BOLD activations if only observing $Z$, $M$, and $R$
without measuring $U$Our Approach: Step 2
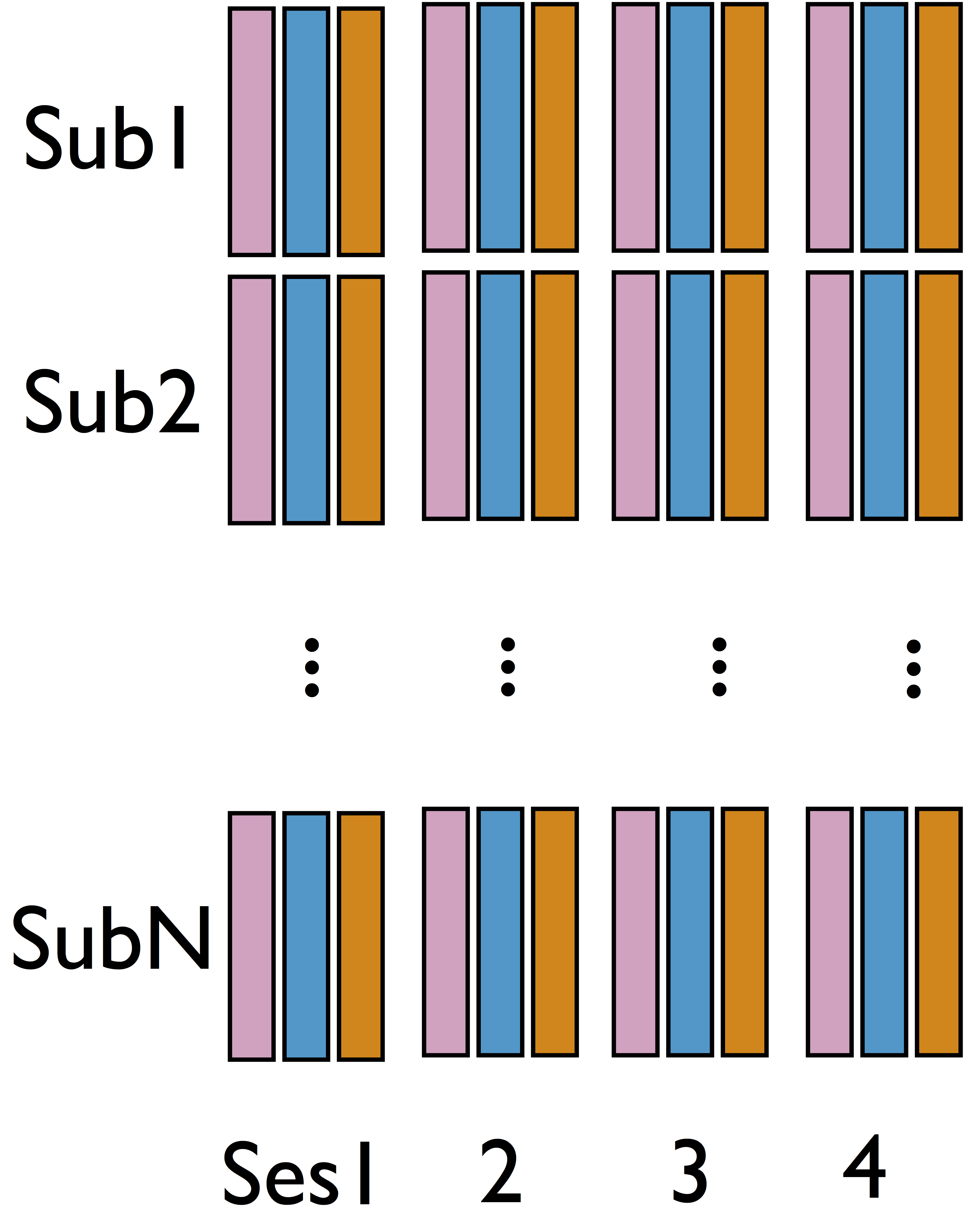
- Cannot identify $\delta$ from single sub and single sess (see our theorem)
- Intuition: leverage complex data structure to infer $\delta$
Step 2: Some Details
- Step 1 model for each sub and each sess
$$\begin{pmatrix}{M}_{ik} & {R}_{ik}\end{pmatrix}=\begin{pmatrix}{Z}_{ik} & {M}_{ik}\end{pmatrix}\begin{pmatrix}{a}_{ik} & {b}_{ik}\\ 0 & {c}_{ik} \end{pmatrix}+\begin{pmatrix}{E}_{1_{ik}} & {E}_{2_{ik}}\end{pmatrix}$$ - Limited variability in $\delta$ across sub/sess
- Random effect model cf AFNI, FSL, SPM, and etc $$\begin{pmatrix}{A}_{ik}\\ {B}_{ik}\\ {C}_{ik} \end{pmatrix}=\begin{pmatrix}{A}\\ {B}\\ {C} \end{pmatrix}+\begin{pmatrix}\alpha_{i}\\ \beta_{i}\\ \gamma_{i} \end{pmatrix}+\begin{pmatrix}\epsilon_{ik}^{{A}}\\ \epsilon_{ik}^{{B}}\\ \epsilon_{ik}^{{C}} \end{pmatrix}=b+u_{i}+\eta_{ik}$$
Option 1: Two-stage Fitting
- Stage 1: fit $(\hat{A}_{ik}(\delta), \hat{B}_{ik}(\delta), \hat{C}_{ik}(\delta))$ for each $i$ and $k$ for varying $\delta$ using our step 1 single-level model
- Stage 2: Find $\hat{\delta}$ that $(\hat{A}_{ik}(\hat{\delta}), \hat{B}_{ik}(\hat{\delta}), \hat{C}_{ik}(\hat{\delta}))$ yields maximum likelihood for random effects model
- Small-scale computing
- However, estimation error in stage 1 not accounted
- Complicates our goal on determining the variance
Option 2: Integrated Modeling
- Optimize all parameters in joint likelihood $$\begin{align*} &\sum_{i=1}^{N}\sum_{k=1}^{K}\log\Pr\left(R_{ik},M_{ik}|Z_{ik},\delta,b_{ik},\sigma_{1_{ik}},\sigma_{2_{ik}}\right)\quad \mbox{Data}\\ & + \sum_{i=1}^{N}\sum_{k=1}^{K}\log\Pr\left(b_{ik}|u_{i},b,\boldsymbol{\Lambda}\right)\quad \mbox{Subject variation}\\ & +\sum_{i=1}^{N}\log\Pr\left(u_{i}|\boldsymbol{{\Psi}}\right) \quad \mbox{Prior}\end{align*}$$
- Large computation: $5NK + 3N + 11 > 2000$ paras
Algorithm
Leverage conditional convexity to reduce computation
details in our paperSimulations
Method Comparison
- Single level models
- BKBaron, Kenny, 86: assuming $\delta = 0$
- CMA-$\delta$ (our single-level method): assuming $\delta = 0$
- Mixed effects multilevel models
- KKBKenny et al, 03: assuming all $\delta = 0$
- CMA-ts (ours): estimating $\delta$, two-stage fitting
- CMA-h, CMA-m (ours): estimating $\delta$, large-scale fitting
- Simulate data with varying $\delta$
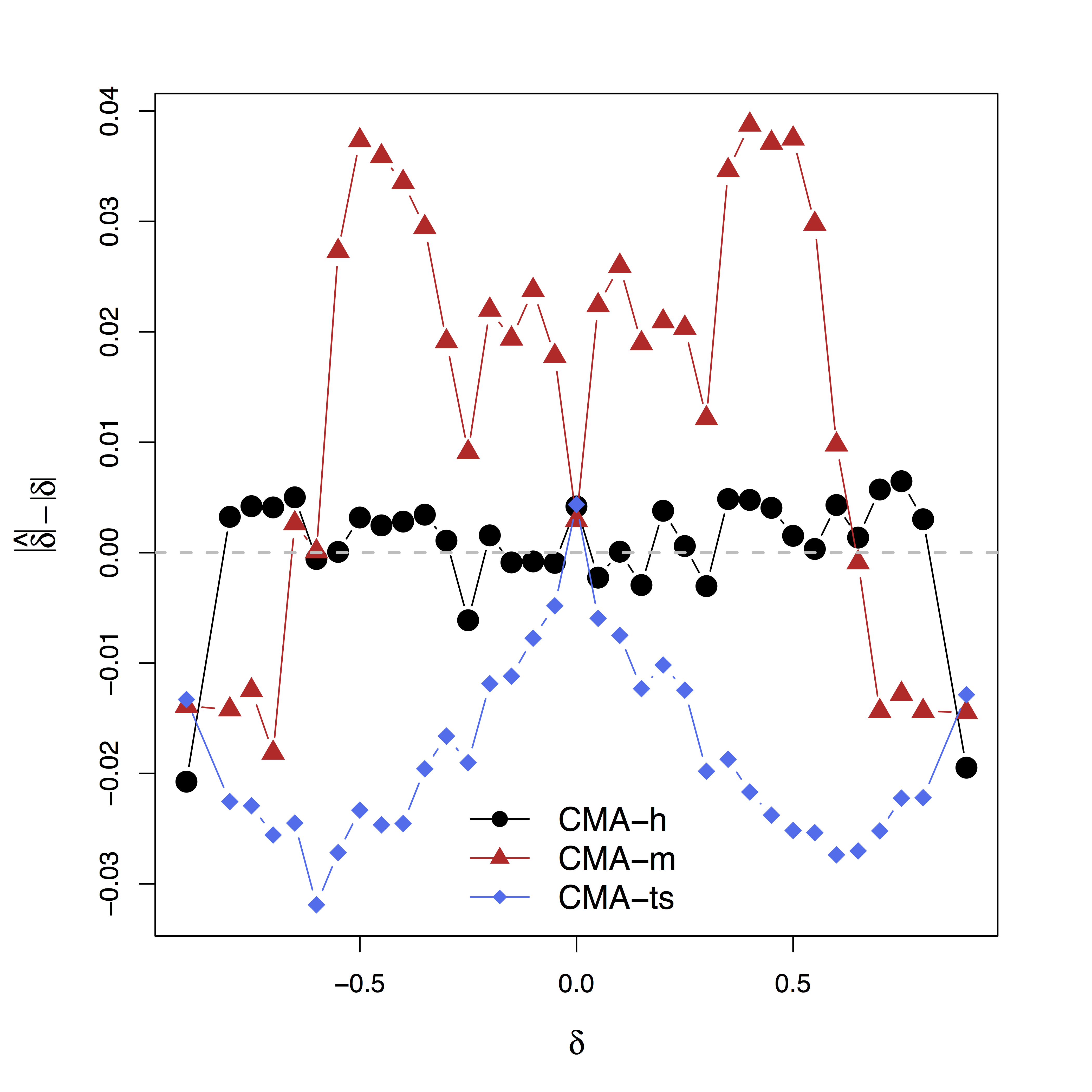
Low bias for $\delta$
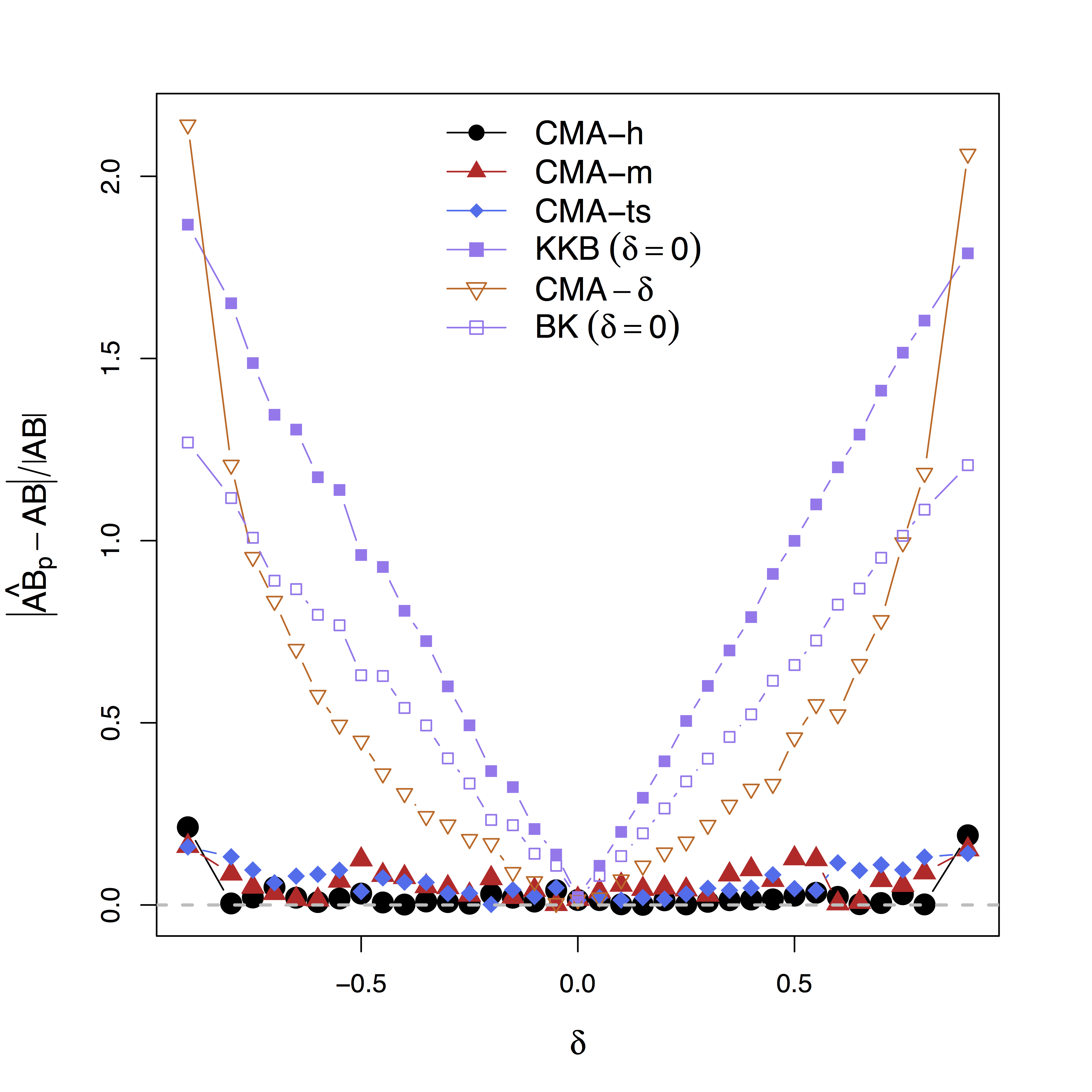
Low bias for effects
Our large-scale multilevel model performs best; Bias can be large (100%) without estimating $\delta$
Real Data
Data
- Random stimuli and scalar activations for each trial
- Stimuli: go = press; stop = not pressing
- stop is expected to suppress motor area (PMC)
- 98 subjects × 4 sessions × 100 trials × 2 regions
- Temporal dependence removed using whitened data and single-trial beta deconvolutionWager et al, 08
Identifiability and Bias
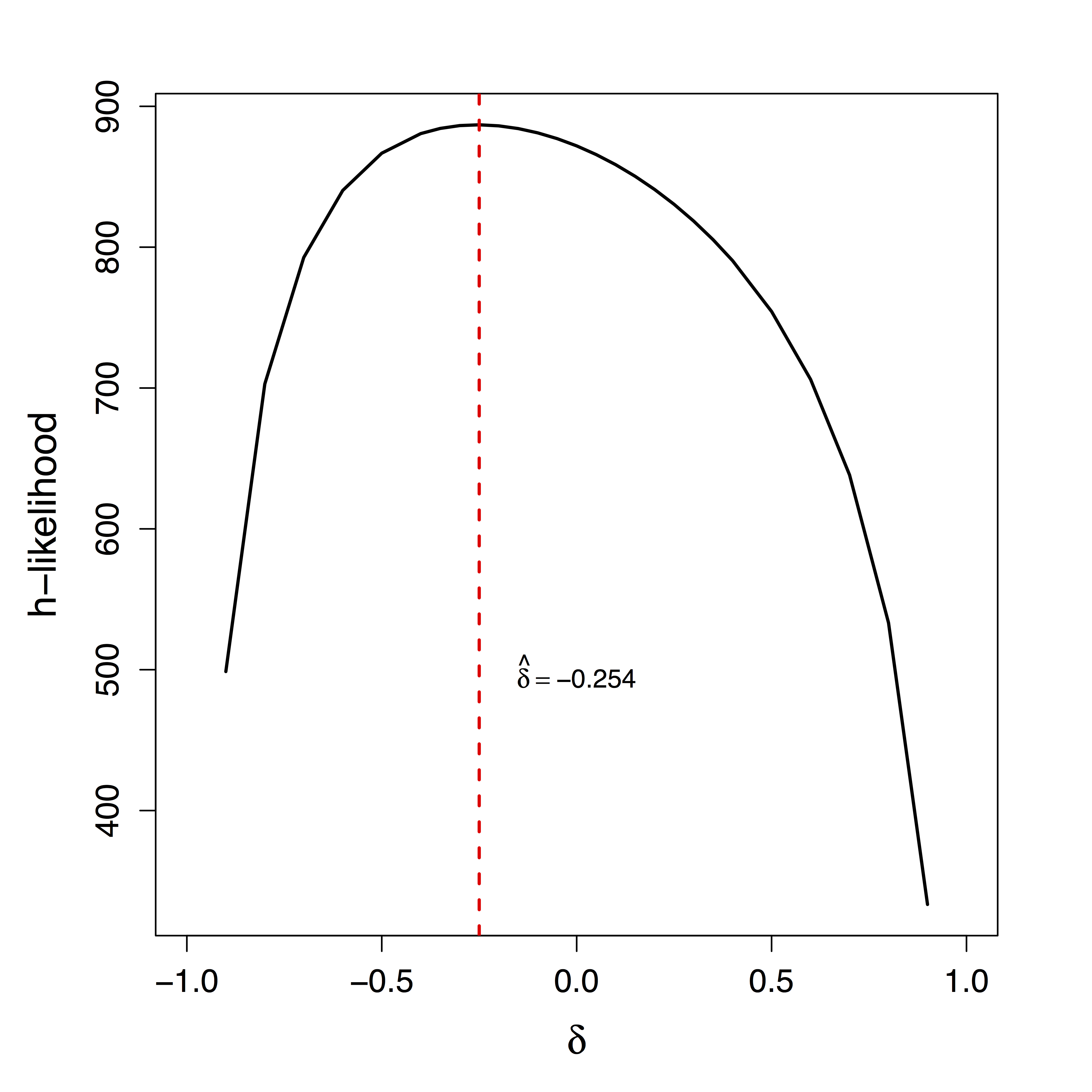
Unique $\delta$ for ML
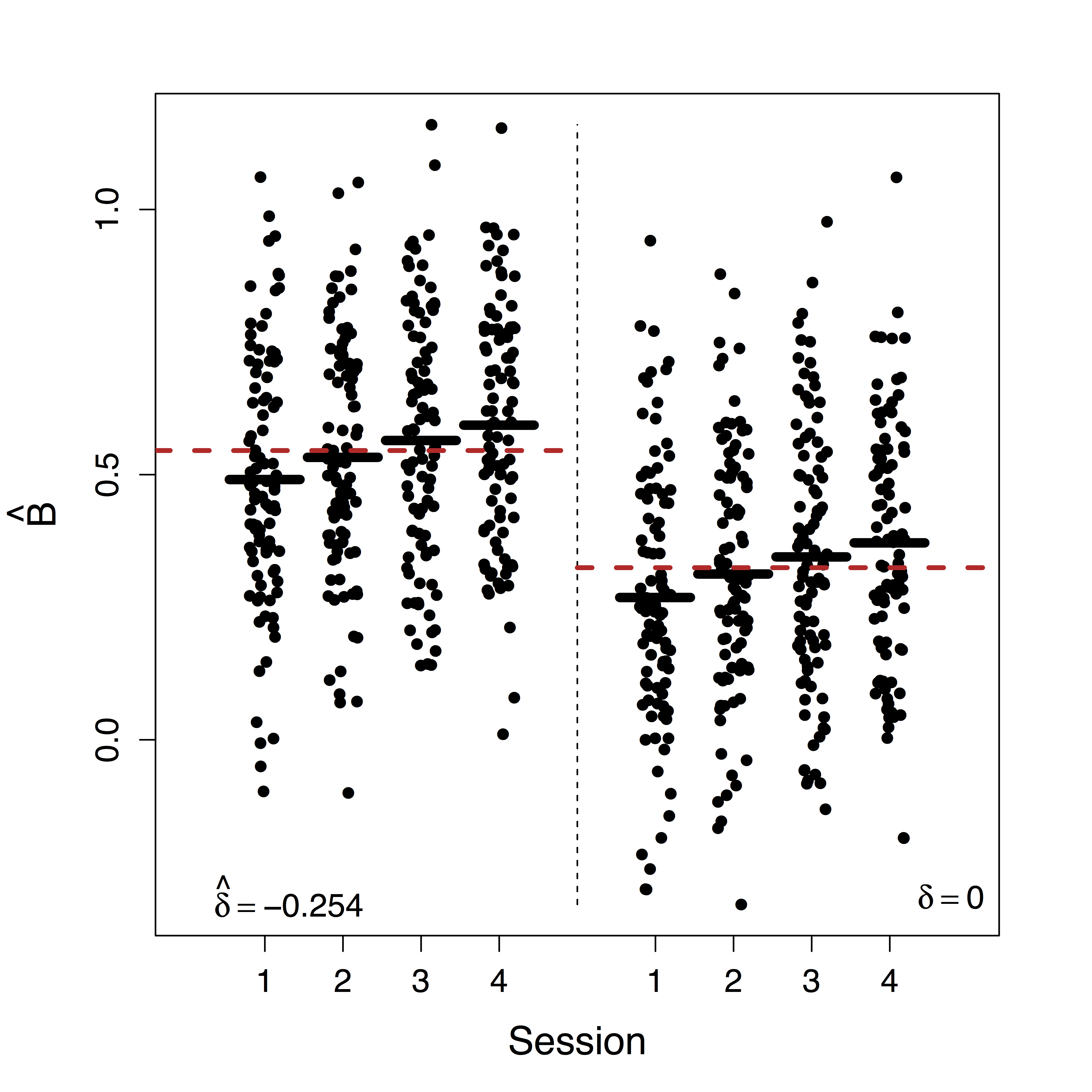
Estimates doubled
- Ours show stop directly suppresses PMC significantly while others do not recover this
- Motion (part of $U$) correction decreases our $\delta$ estimate but do not change our causal estimates
Summary
- Leverage complex data for causal fMRI modeling
- Approach:
large-scale causal SEM + big multilevel data +machine learning/optimization - Theory: identifiability, convergence, and computation
- Result: reduced bias and improved interpretation
- Extensions: temporal models, identifiability conditions, multiple pathwaysPathway Lasso, our arXiv 1603.07749
- Manuscript:
Consistent Mediation Analysis , 2015 ENAR Student Paper Award, revision for JASA, (arXiv 1410.7217)
Thank you!
Slides at: bit.ly/xlSAMSI16
