Big Complex Data, Causality,
and Brain Pathways
Xi (Rossi) Luo
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science
ABCD Research Group

Sanya, CHINA
December 27, 2016
Funding: NIH R01EB022911; NSF/DMS (BD2K) 1557467; NIH P20GM103645, P01AA019072, P30AI042853; AHA
Coauthor

Yi Zhao
(4rd Yr PhD Student,
Receipient of multiple student awards, including the 2015 ENAR distinguished paper
Brown University
Math Problem:
Infer Causality from Obs. Data Only
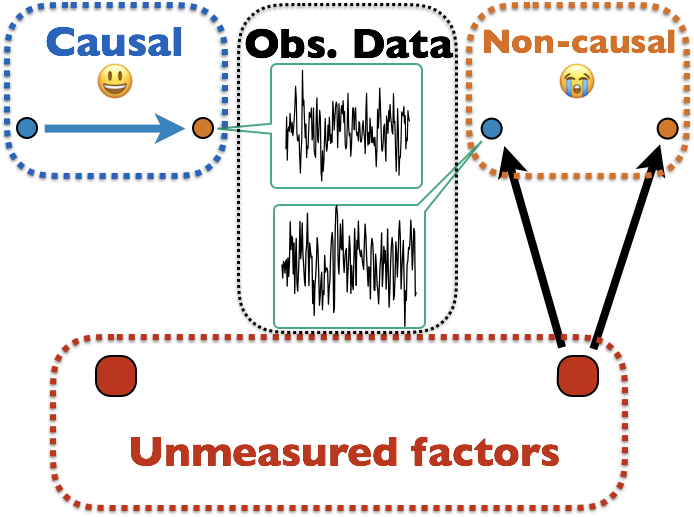
Many unmodeled factors: vascular, respriatory, mind wandering, ...
Stop/Go Task fMRI
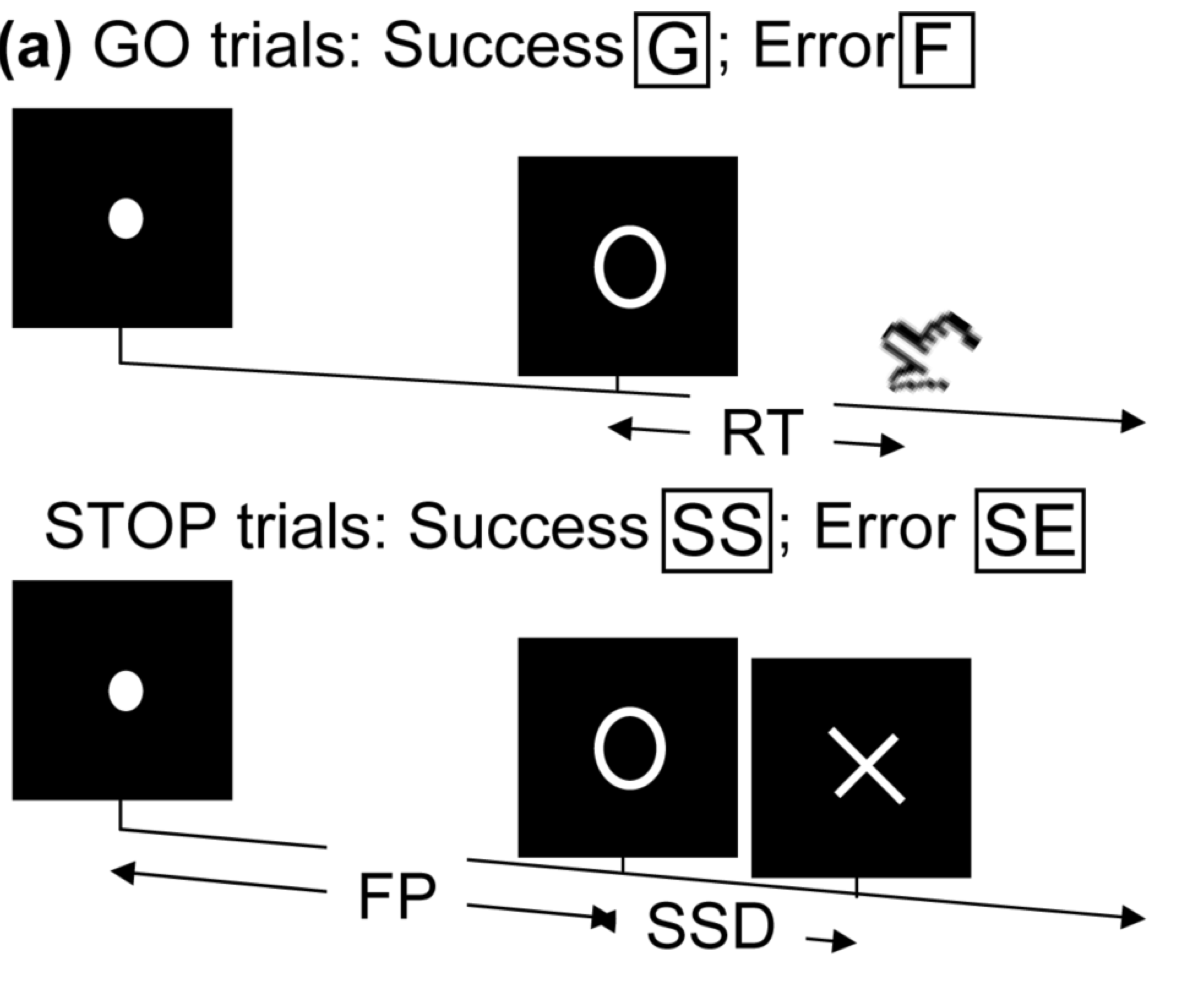
- Task fMRI: performs tasks under brain scanning
-
Randomized stop/go task:- press button if "go";
- withhold pressing if "stop"
- Not resting-state: "rest" in scanner
fMRI data: blood-oxygen-level dependent (BOLD) signals from each
Raw Data: Motor Region
fMRI Studies
Sub 1, Sess 1

Time 1

2
…

~300
⋮
Sub i, Sess j


…

⋮
Sub ~100, Sess ~4


…

Our data: 98 subjects × 4 sessions × 100 trials × 2 regions
Question: can "big and complex" fMRI data be helpful?
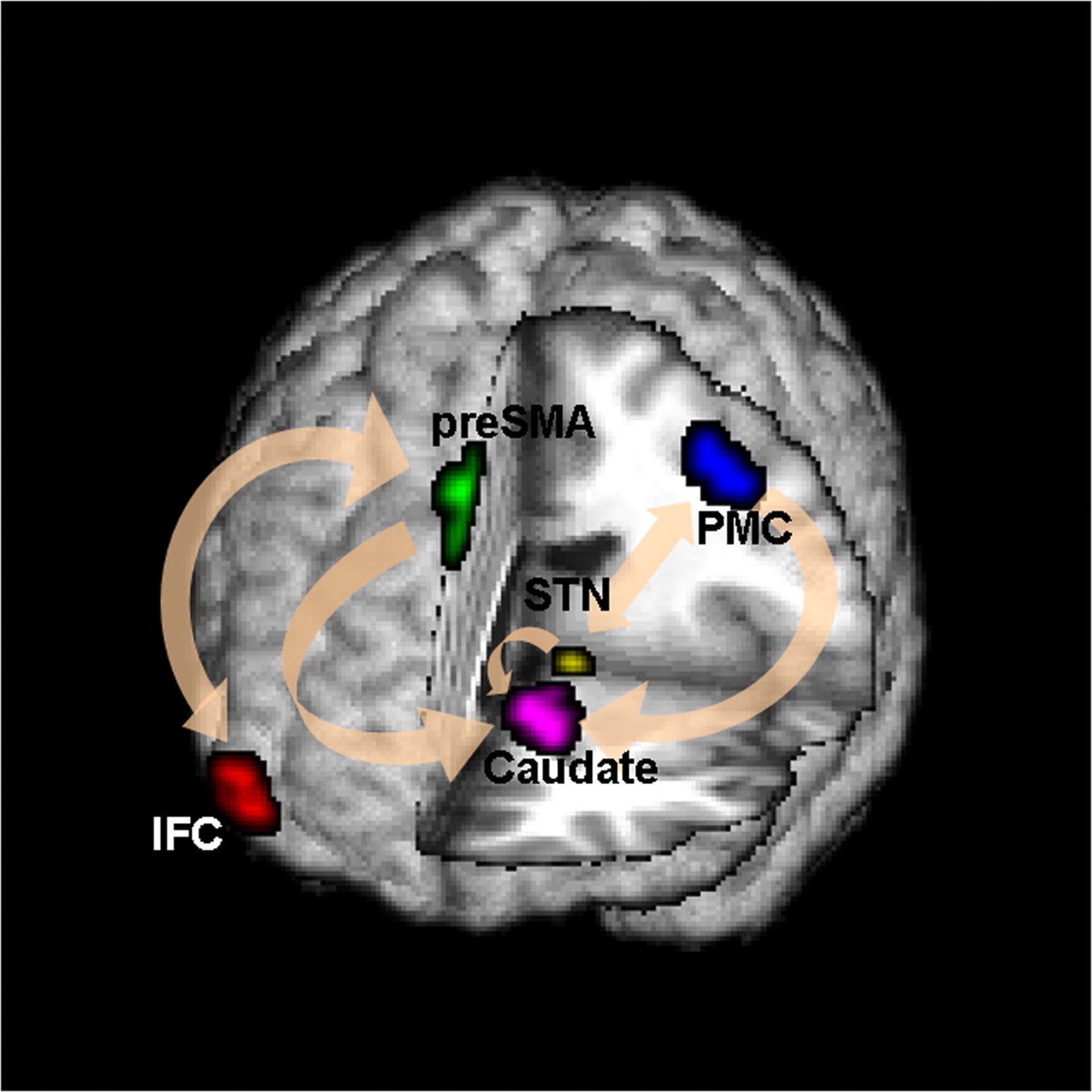
Brain Networks
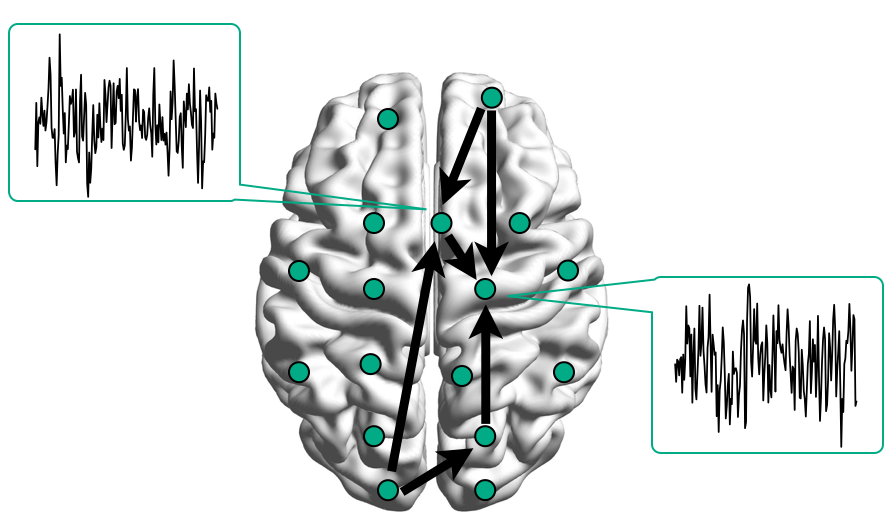
Functional/Effective Connectivity
Network Model with Stimulus
Goal: quantify effects stimuli → preSMA → PMC regions Duann, Ide, Luo, Li (2009). J of Neurosci
Model
Mediation Analysis and SEM
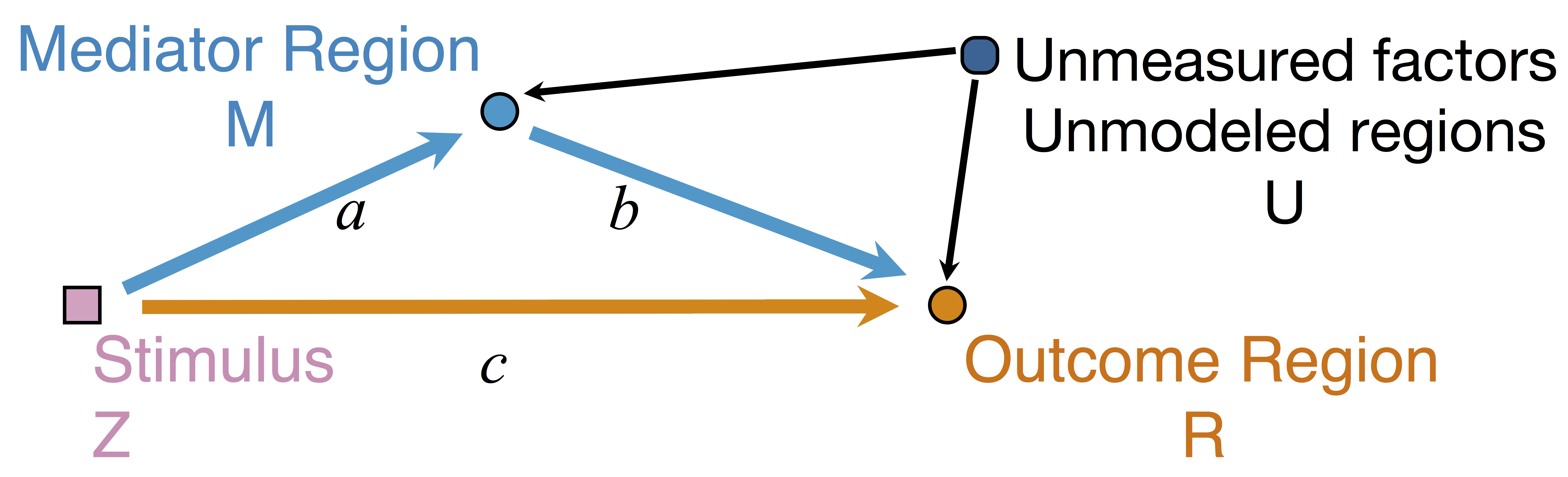 $$\begin{align*}M &= Z a + \overbrace{U + \epsilon_1}^{E_1}\\ R &= Z c + M b + \underbrace{U g + \epsilon_2}_{E_2}, \quad \epsilon_1 \bot \epsilon_2\end{align*}$$
$$\begin{align*}M &= Z a + \overbrace{U + \epsilon_1}^{E_1}\\ R &= Z c + M b + \underbrace{U g + \epsilon_2}_{E_2}, \quad \epsilon_1 \bot \epsilon_2\end{align*}$$
-
Indirect effect: $a \times b$; Direct effect: $c$ - Correlated errors: $\delta = \cor(E_1, E_2) \ne 0$ if $U\ne 0$
Mediation Analysis in fMRI
- Mediation analysis (usually assuming $U=0$)
- Baron&Kenny, 86; Sobel, 82; Holland 88; Preacher&Hayes 08; Imai et al, 10; VanderWeele, 15;...
- Parametric Wager et al, 09 and functional Lindquist, 12 mediation, under (approx.) independent errors
- Stimulus $\rightarrow$ brain $\rightarrow$ user reported ratings, one brain mediator
- Assuming $U=0$ between ratings and brain
- Multiple mediator and multiple pathways
- Dimension reduction by arXiv1511.09354Chen, Crainiceanu, Ogburn, Caffo, Wager, Lindquist, 15
- Pathway Lasso penalization Zhao, Luo, 16
- This talk: causal estimation under $U\ne 0$ (its effect size $\delta \ne 0$) when modeling two brain regions

Existing Approaches for $\delta \ne 0$
- Assuming $\delta=0$
- Assumption "too strong" for most cases Imai et al, 10
- Sensitivity plot: "guessing" $\delta$
- Simplify models: e.g. $c=0$ via instrumental variable
- Adjust (e.g. motion) if possible Sobel, Lindquist, 14
- Use Bayesian prior or regularization
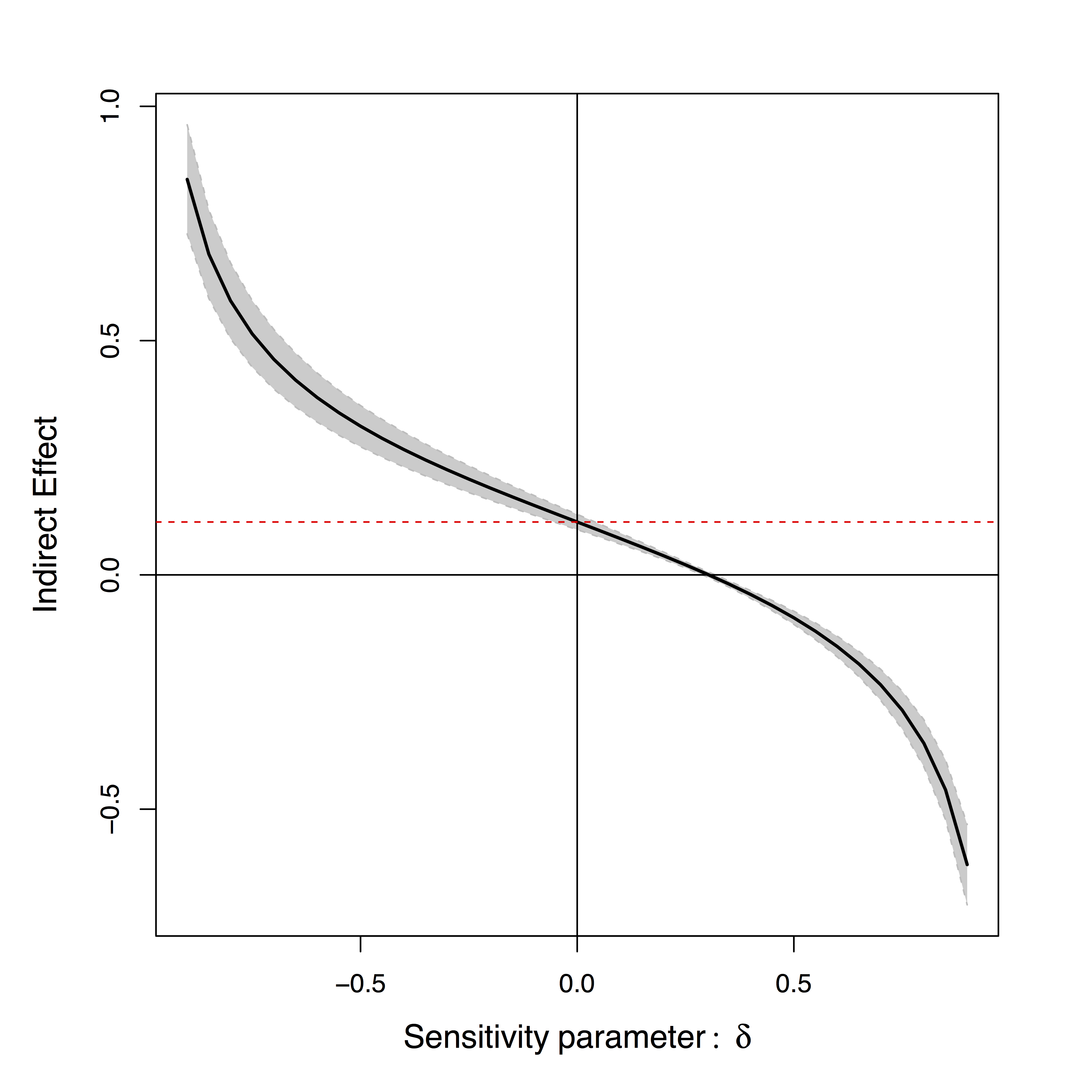
Positive or negative effects depending on subjective choice of $\delta$
Method
Our Approach: Step 1
- Bivariate
single-level model $$\begin{align*}\begin{pmatrix}M & R\end{pmatrix} & = \begin{pmatrix}Z & M\end{pmatrix} \begin{pmatrix}a & c\\ 0 & b \end{pmatrix} + \begin{pmatrix}E_{1} & E_{2}\end{pmatrix}\\ (E_1, E_2) & \sim MVN(\boldsymbol{0}, \boldsymbol{\Sigma}) \quad \boldsymbol{\Sigma}=\begin{pmatrix}\sigma_{1}^{2} & \delta\sigma_{1}\sigma_{2}\\ \delta\sigma_{1}\sigma_{2} & \sigma_{2}^{2} \end{pmatrix} \end{align*}$$ - Estimate $(a,b,c,\boldsymbol{\Sigma})$ via ML (a lot of handwaving)
- We solve an optimization with constraints
- Different than running two regressions
Causal Interpretation
- Prove causal using potential outcomes Neyman, 23; Rubin, 74
- Causal inference intuition $$Z \rightarrow \begin{pmatrix} M \\ R \end{pmatrix}$$
- Others assume (e.g. randomized brain stimulation) $$r_{i}\left(z_{i}^{\prime},m_{i}\right)\bot m_{i}\left(z_{i}\right)|Z_{i}=z_{i}$$
- We do
not need this assumption given $\delta$
Theory
- Theorem:
Given $\delta$, unique maximizer of likelihood, expressed in closed form - Theorem:
Given $\delta$, our estimator is root-n consistent and efficient - Bias (and variance) depends on $\delta$
Maximum Likelihood: “Tragedy may lurk around a corner”
[Stigler 2007]"Tragedy" of ML
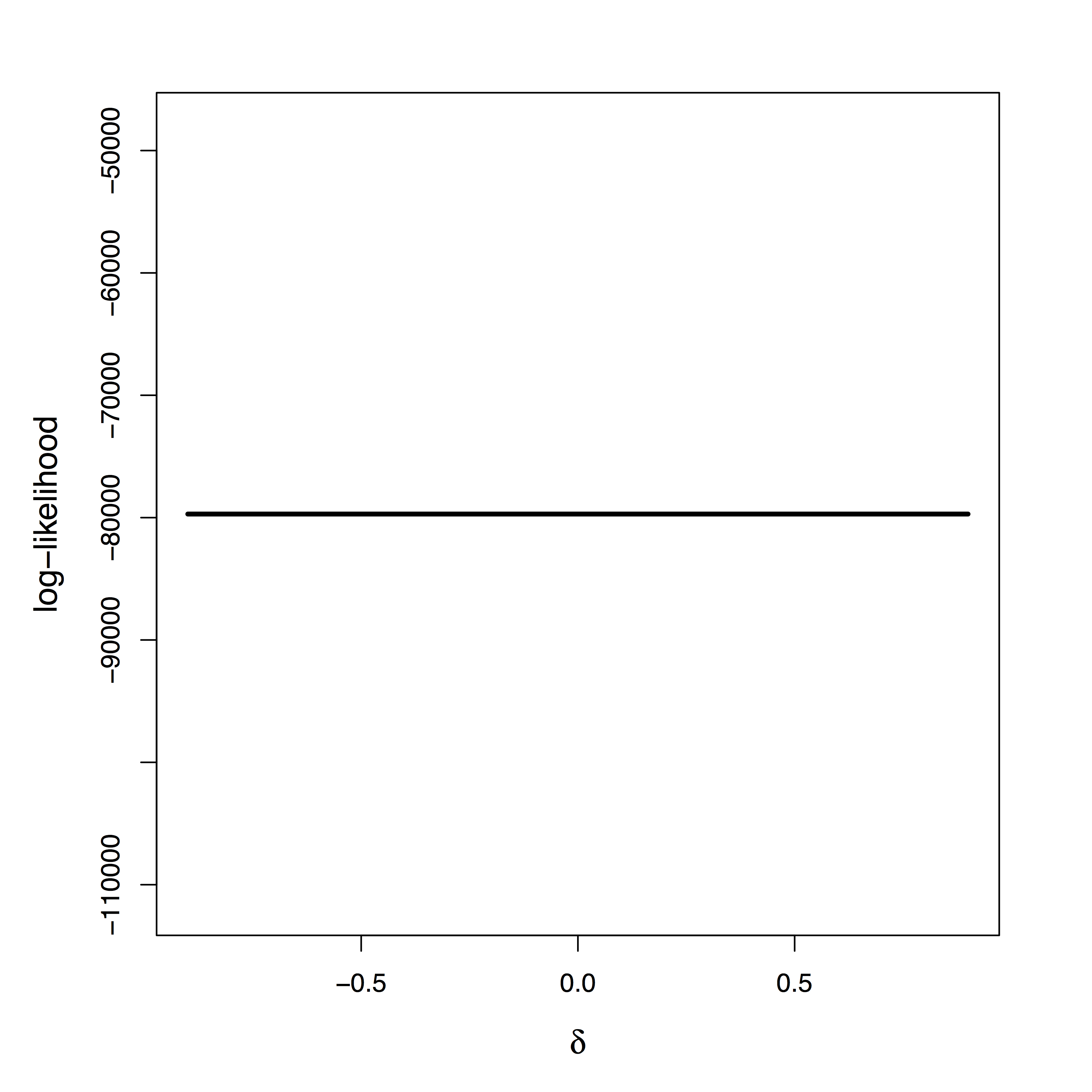
- Likelihood provides
zero info about $\delta$ - Cannot simply apply priors on $\delta$
Two different models generate same single-trial BOLD activations if only observing $Z$, $M$, and $R$
without measuring $U$Our Approach: Step 2
- Cannot identify $\delta$ from single sub and single sess (see our theorem)
- Intuition: leverage complex data structure to infer $\delta$
Step 2: Some Details
- Step 1 model for each sub and each sess
$$\begin{pmatrix}{M}_{ik} & {R}_{ik}\end{pmatrix}=\begin{pmatrix}{Z}_{ik} & {M}_{ik}\end{pmatrix}\begin{pmatrix}{a}_{ik} & {b}_{ik}\\ 0 & {c}_{ik} \end{pmatrix}+\begin{pmatrix}{E}_{1_{ik}} & {E}_{2_{ik}}\end{pmatrix}$$ - Limited variability in $\delta$ across sub/sess
- Random effect model cf AFNI, FSL, SPM, and etc $$\begin{pmatrix}{A}_{ik}\\ {B}_{ik}\\ {C}_{ik} \end{pmatrix}=\begin{pmatrix}{A}\\ {B}\\ {C} \end{pmatrix}+\begin{pmatrix}\alpha_{i}\\ \beta_{i}\\ \gamma_{i} \end{pmatrix}+\begin{pmatrix}\epsilon_{ik}^{{A}}\\ \epsilon_{ik}^{{B}}\\ \epsilon_{ik}^{{C}} \end{pmatrix}=b+u_{i}+\eta_{ik}$$
Option 2: Integrated Modeling
- Optimize all parameters in joint likelihood $$\begin{align*} &\sum_{i=1}^{N}\sum_{k=1}^{K}\log\Pr\left(R_{ik},M_{ik}|Z_{ik},\delta,b_{ik},\sigma_{1_{ik}},\sigma_{2_{ik}}\right)\quad \mbox{Data}\\ & + \sum_{i=1}^{N}\sum_{k=1}^{K}\log\Pr\left(b_{ik}|u_{i},b,\boldsymbol{\Lambda}\right)\quad \mbox{Subject variation}\\ & +\sum_{i=1}^{N}\log\Pr\left(u_{i}|\boldsymbol{{\Psi}}\right) \quad \mbox{Prior}\end{align*}$$
- Large computation: $5NK + 3N + 11 > 2000$ paras
Algorithm
Leverage conditional convexity to reduce computation
details in our paperTheory for SEM and Confounding
Contributions: data-driven estimation of confounding and consistency in SEM
Simulations
Method Comparison
- Single level models
- BKBaron, Kenny, 86: assuming $\delta = 0$
- CMA-$\delta$ (our single-level method): assuming $\delta = 0$
- Mixed effects multilevel models
- KKBKenny et al, 03: assuming all $\delta = 0$
- CMA-ts (ours): estimating $\delta$, two-stage fitting
- CMA-h, CMA-m (ours): estimating $\delta$, large-scale fitting
- Simulate data with varying $\delta$
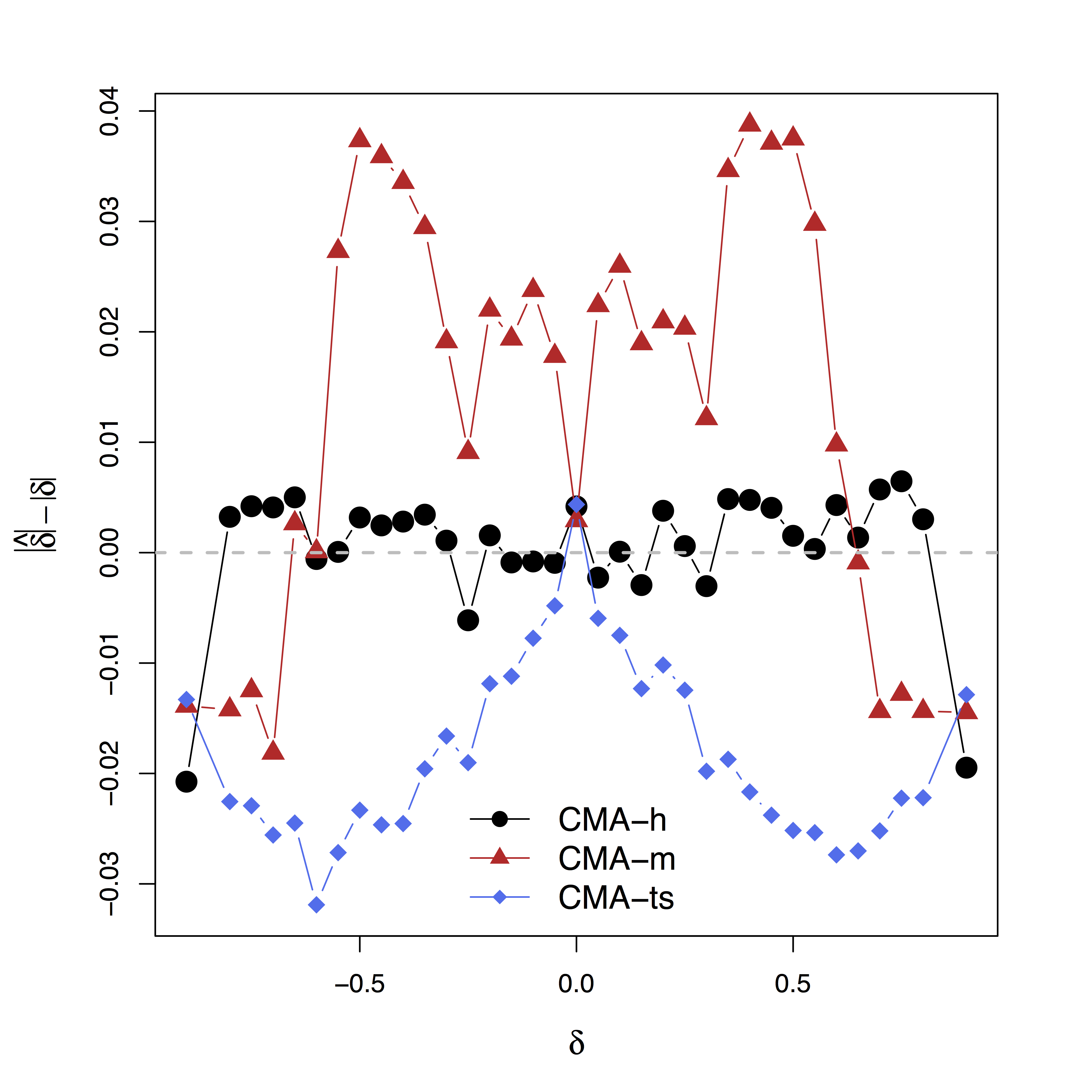
Low bias for $\delta$
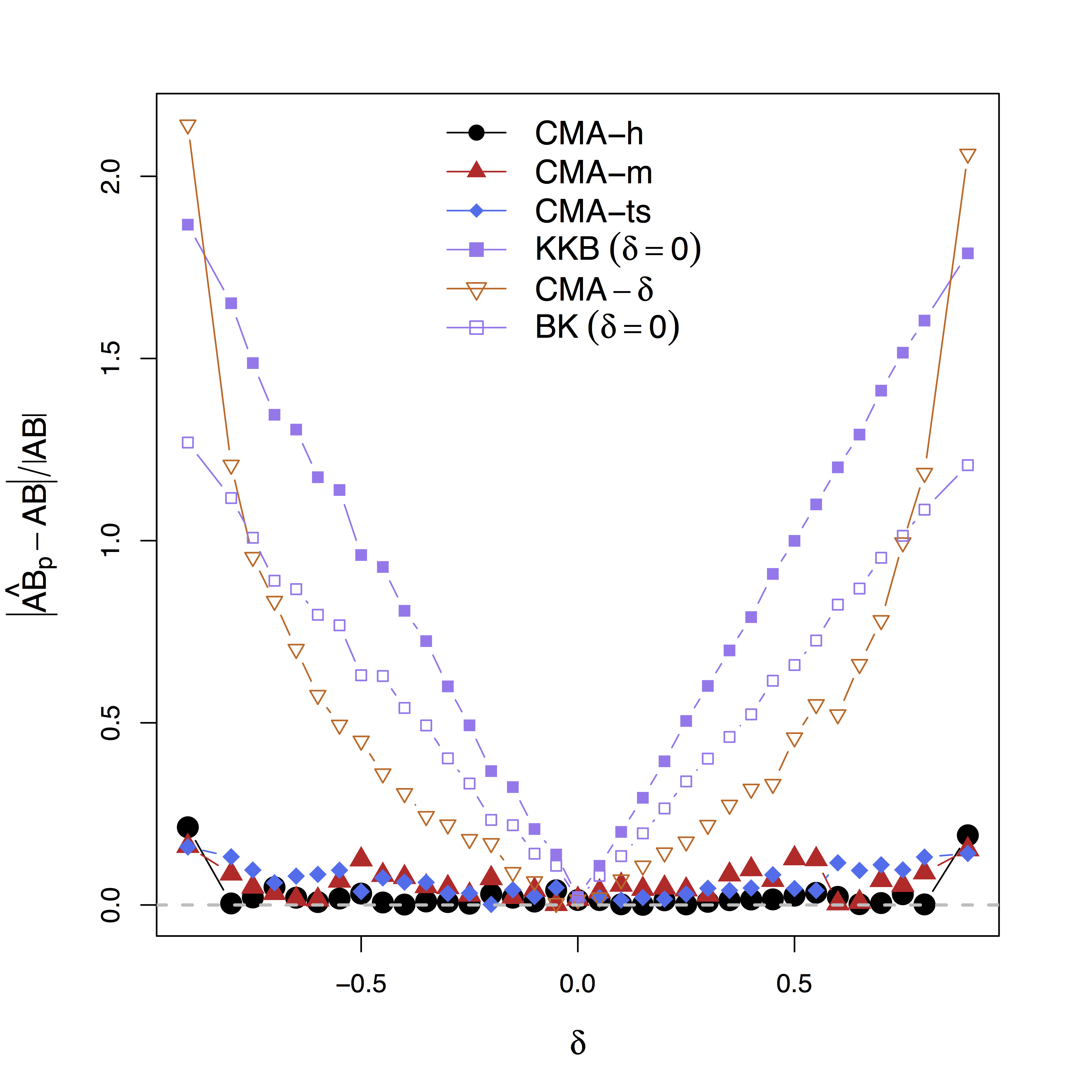
Low bias for effects
Our large-scale multilevel model (
Bias can be large (100%) without estimating $\delta$
Real Data
Data
- Random stimuli and scalar activations for each trial
- Stimuli: go = press; stop = not pressing
- stop is expected to supress motor area (PMC)
- 98 subjects × 4 sessions × 100 trials × 2 regions
- Temporal dependence removed using whitened data and single-trial beta deconvolutionWager et al, 08
Identifiability and Bias
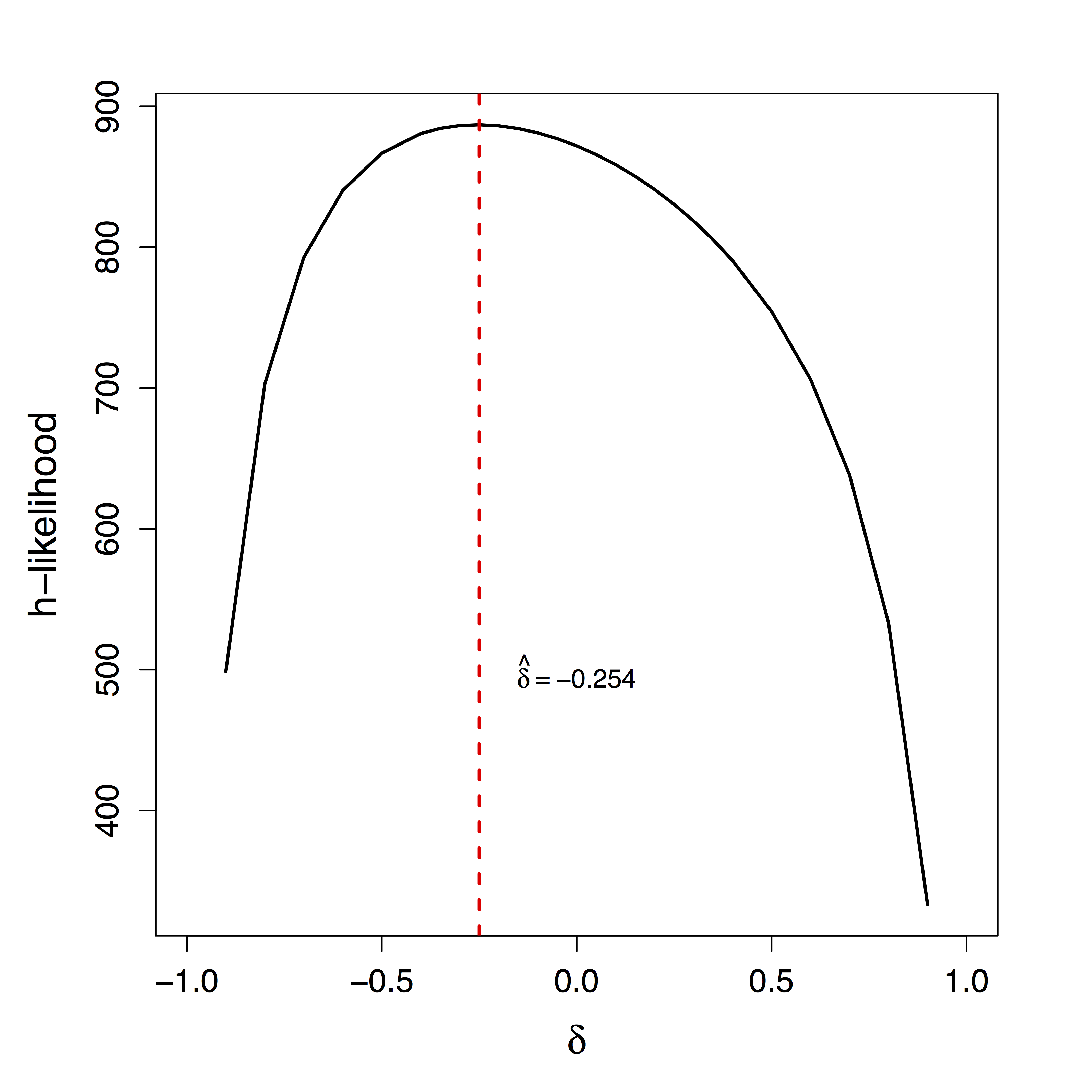
Unique $\delta$ for ML
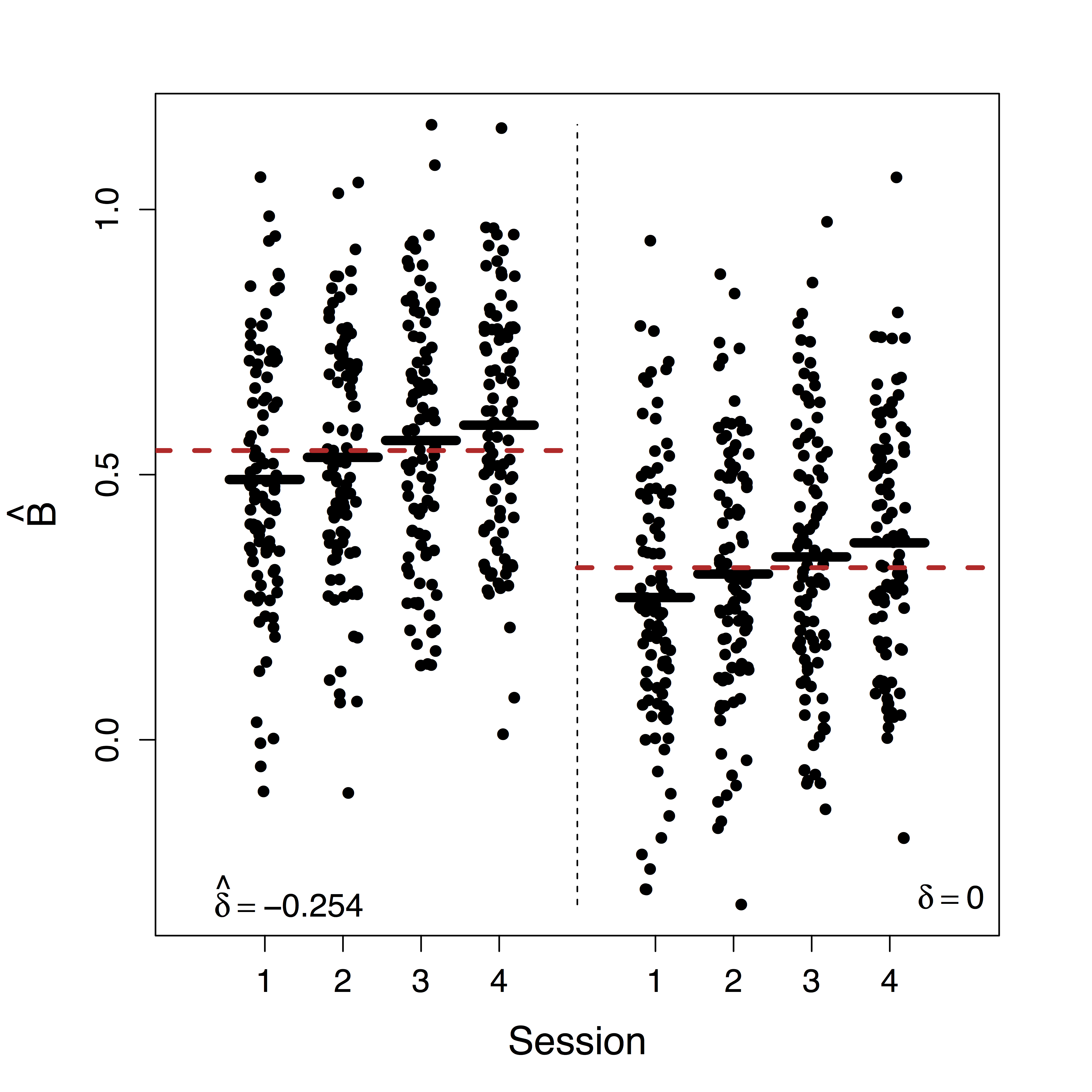
Estimates doubled
- Ours show stop directly supresses PMC significantly while other methods fail to recover this
- Motion (part of $U$) correction decreases our $\delta$ estimate but do not change our causal estimates
Summary
- Leverage complex data for causal fMRI modeling
- Approach:
-
large-scale causal SEM - big multilevel data
-
machine learning/optimization
-
- Theory: identifiability, convergence, and computation
- Result: reduced bias and causal interpretation
Discussion
- Extensions: temporal models, functional models, multiple pathwaysPathway Lasso, our arXiv 1603.07749
- Manuscript: 2015 ENAR Student Paper Award, revision for JASA, (arXiv 1410.7217)
- R package:
macc

c ausality
Thank you!
Slides at: bit.ly/sanya16

More info: Big Complex Data.com
Postdoc position available
funded by Obama's