Binary Autoregressive Network Modeling of Comorbidity Networks from Electronic Health Records

Xi (Rossi) LUO

The University of Texas
Health Science Center
School of Public Health
Dept of Biostatistics
and Data Science

ICSA, Houston
December 15, 2020

Funding: NIH R01EB022911 and UT Health Start-up Fund

Slides viewable on web:
bit.ly/ehrnet20

or

BigComplexData.com

Co-Authors

Gen Zhu
UT Health, BADS

Hulin Wu
UT Health, BADS

EHR Data: Medical Encounter/Diagnosis

Time

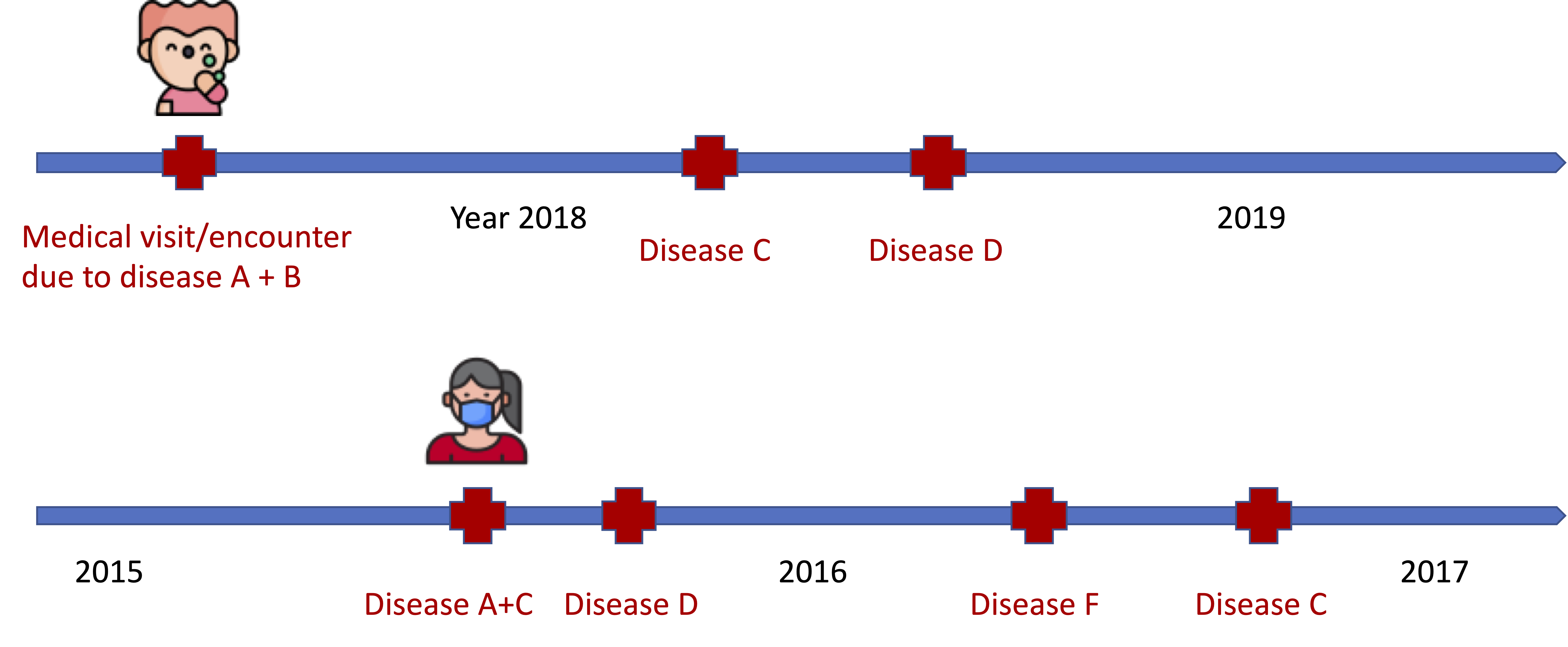
Challenges

• Many many unique diagnosis codes (~100K)
• Large but heterogeneous samples (~10K to ~10M)
• In a nutshell, time series of events from a huge number of types
• Many other associated data types (lab, prescription)

Method

Existing Methods for Inferring Comorbidity Networks

• Most existing methods are pair-wise Fotouhi et al. 2018
• $w_{ij}$ be freq of disease $i$ happens prior to disease $j$
• Define link weights: $$s_x^{o} = \sum_y w_{xy}, \quad s_x^{i} = \sum_y w_{xy}, \quad, s = \sum_{xy} w_{xy}, $$
• $\phi$-correlation and OER: $$ \phi_{ij} = \frac{w_{ij} s - s_i^{o} s_j^{i}}{\sqrt{s_i^{o} s_j^{i} (s - s_i^{o}) (s - s_i^{i}) }}, \quad OER_{ij} = \frac{w_{ij}s}{s_j^{i} s_i^{o}} $$
• Univariate logistic regression Aguado et al. 2020
• First talk in this session by Dr Maroufy and colleagues

Limitations

• Pair-wise associations fail to adjust other intermediate diseases developed in-between
• Multiple testing issues due to a large number of diseases $O(p^2)$
• Partially account for the temporal order
  • Disease A, B, C may happen in a specific temporal order

Model

• We use ICD-9 codes for diagnoses
• $y_{ijk} = 1$ if patient $i$ has diagnosis code $k$ at encounter $j$, vector $Y_{ij}$ for all diagnosis codes
  • Also known as one-hot encoding
• Binary autoregressive model
$$ P(y_{ijk} = 1 | Y_{i,j-1}) = (1 + \exp(-Y_{i,j-1}^T \beta_k ) )^{-1} $$
• Inspired by Granger/vector autoregressive models for continuous variables
• $\beta_k$ denotes how each past diesase predicts future diagnosis $k$

Conditional Likelihood

• Full likelihood is challenging to compute
• Propose to optmize the penalized log-likelihood: $$\min_{\beta_k} \sum_{ij} \ell(y_{ijk} | \beta_k ) + \lambda \| \beta_k \|_1 $$
• Similar to Ising graphical models for binary data without temporal ordering Ravikumar et al, 10; van de Geer et al, 14
• Implementation: LASSO penalized logistic regression

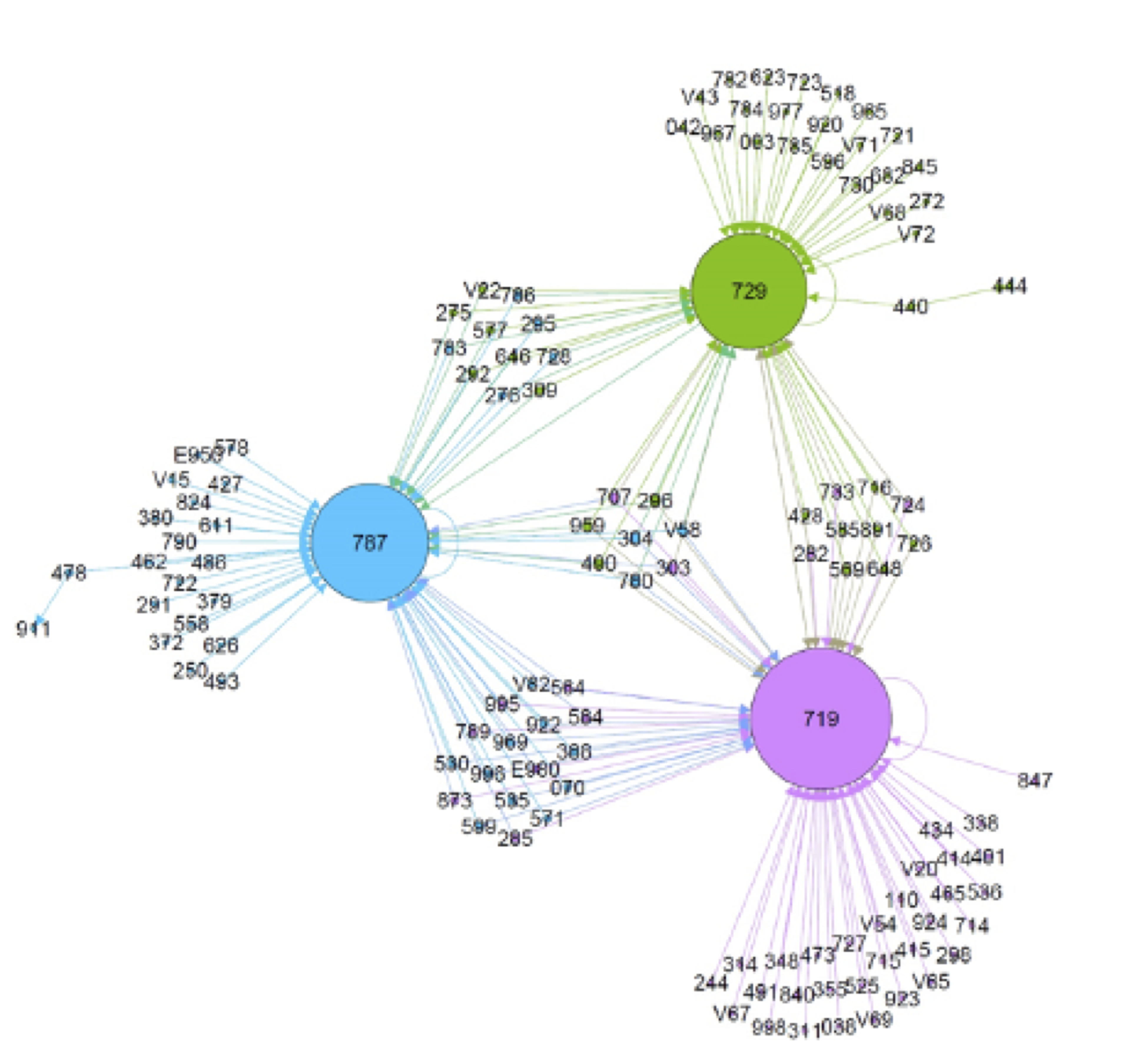
Real Data

Cerner's EHR

• Purchased EHR data by UT Health, Center for Big Data in Health Sciences, Director Dr. Hulin Wu
• Huge dataset: >60M paitients, ~1 billion diagnoses
• Small dataset of patients with drug overdose diagnosis
• 640 diseases, 11481 patients
• Goal: find network of diseases prior or after drug overdose

Simulations

Comparision with Other Methods

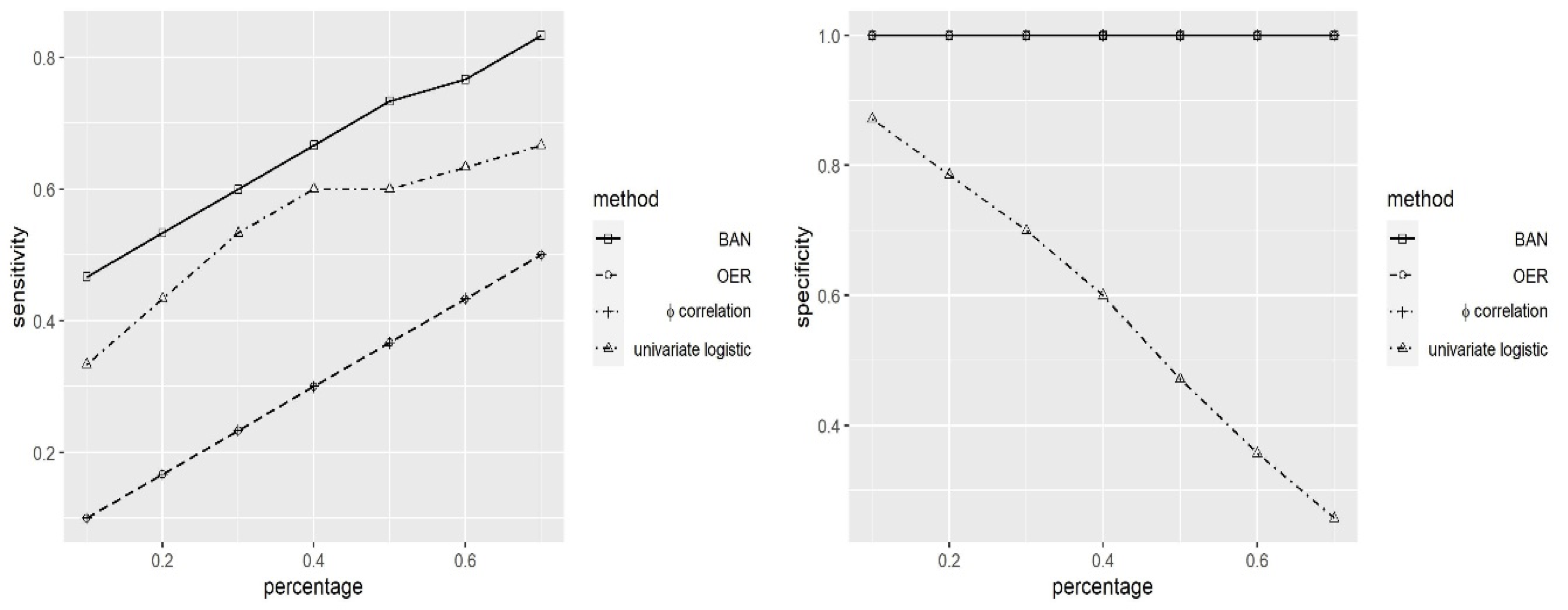
Discussion

• Model inspired by real-world EHR data
• Recovered directional disease networks
• Method: Granger causality + Ising models + ML
  • high dimensionality, sparsity and temporality
• Many future directions:
  • Bottle neck: managing and extracting data
  • Lots of opportunities for theory and method

Thank you!

Comments? Questions?