Some Challenges in Causal Mediation from fMRI


Xi (Rossi) LUO


The University of Texas
Health Science Center at Houston
School of Public Health
Dept of Biostatistics and Data Science


IMSI, Univ of Chicago, USA
August 28, 2024

Funding: NIH R01MH126970, R01EB022911

fMRI Experiments

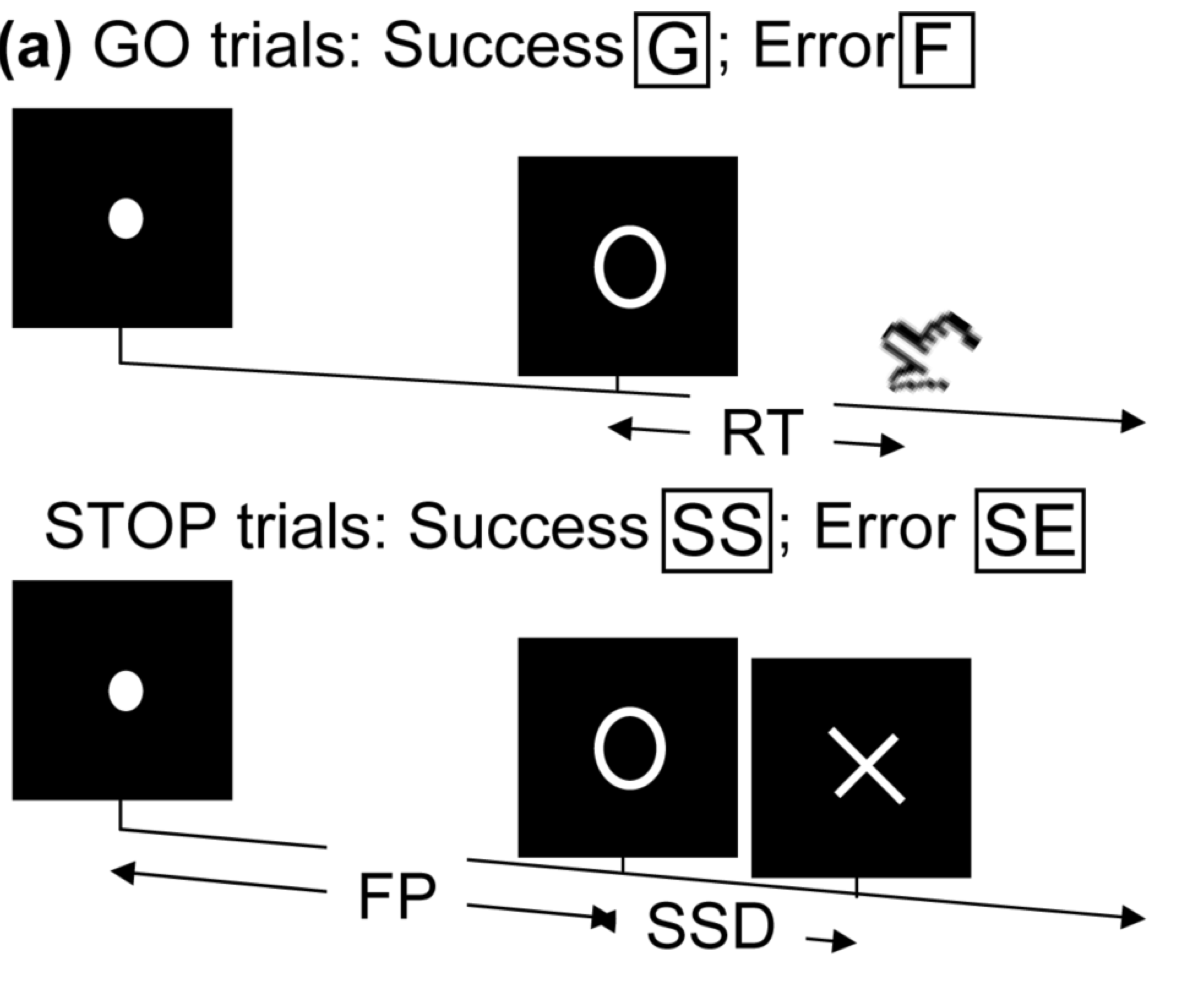
  • Task fMRI: performs tasks under brain scanning
  • Randomized stop/go task:
    • press button if "go";
    • withhold pressing if "stop"
  • Resting-state fMRI: "do nothing" during scanning


Challenging to infer causality from noisy, indirect fMRI measures

Judea Pearl wrote: in The Causal Foundations of Structural Equation Modeling

...causal effects in observational studies can only be substantiated from a combination of data and untested theoretical assumptions, not from the data alone.

Multilevel fMRI Studies

Subject 1, Session 1

Time 1

2

…

~T


⋮

Subject i, Session j

…

⋮

Sub N, Sess K

…

Subject x Session x Time, millions of data points

Brain Mediation Model

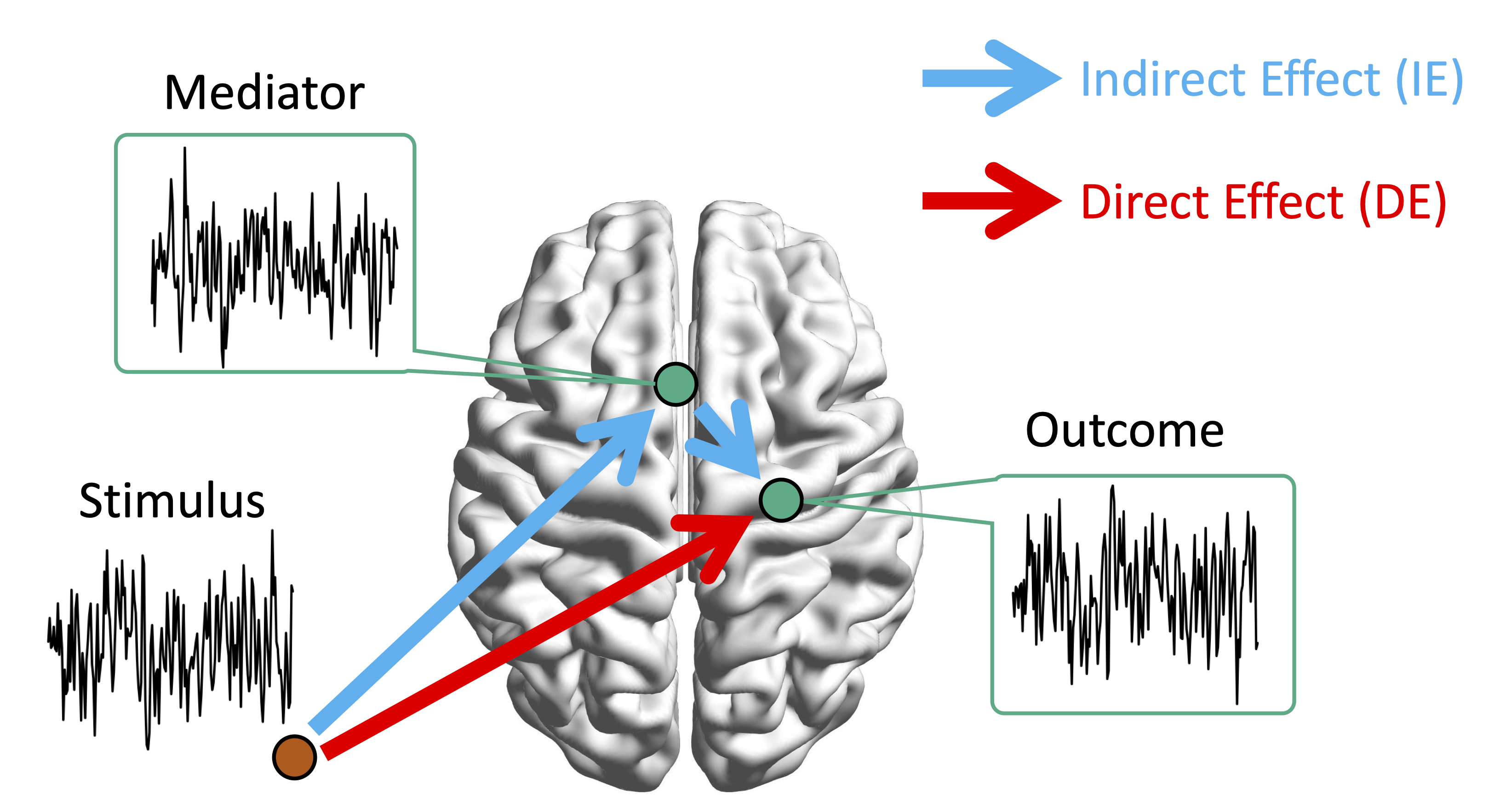
Goal: quantify the direct and indirect effects

Scalar Mediation using SEM

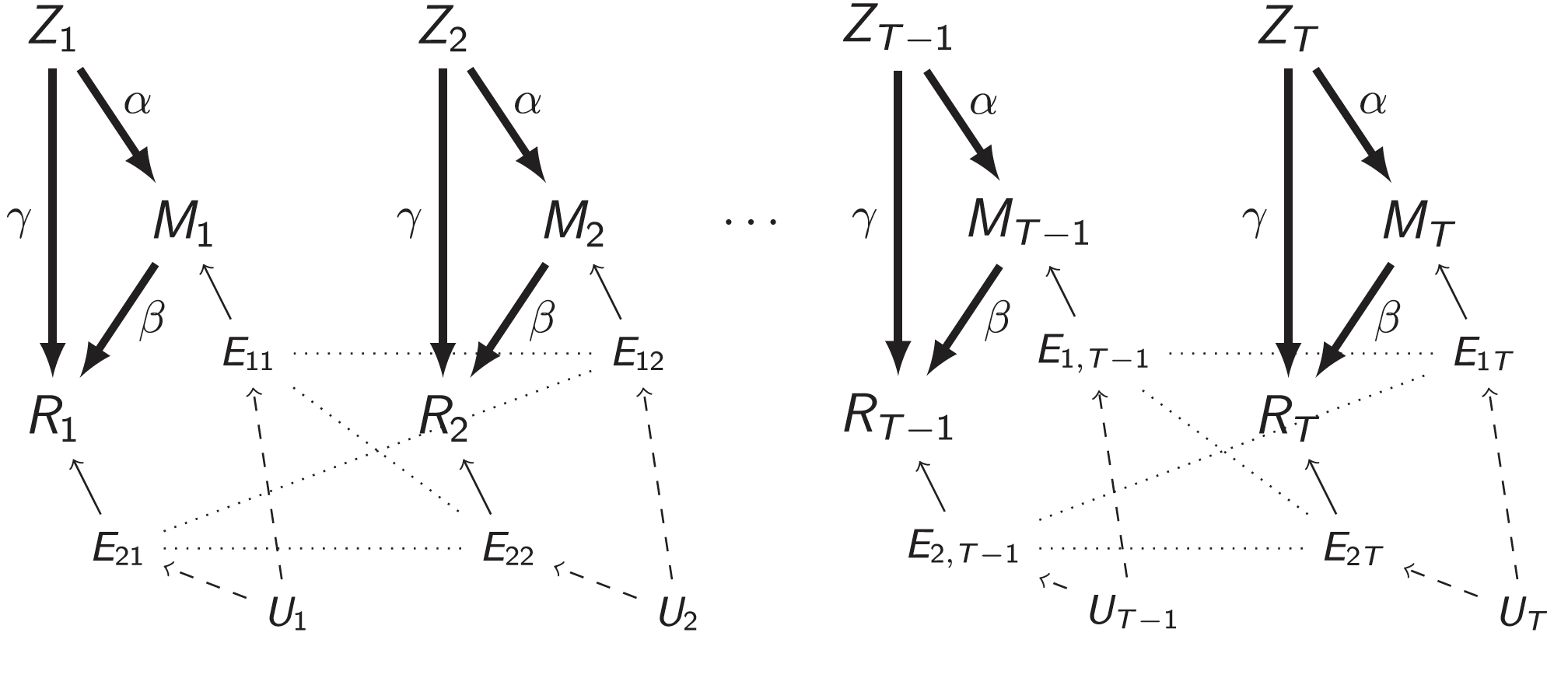
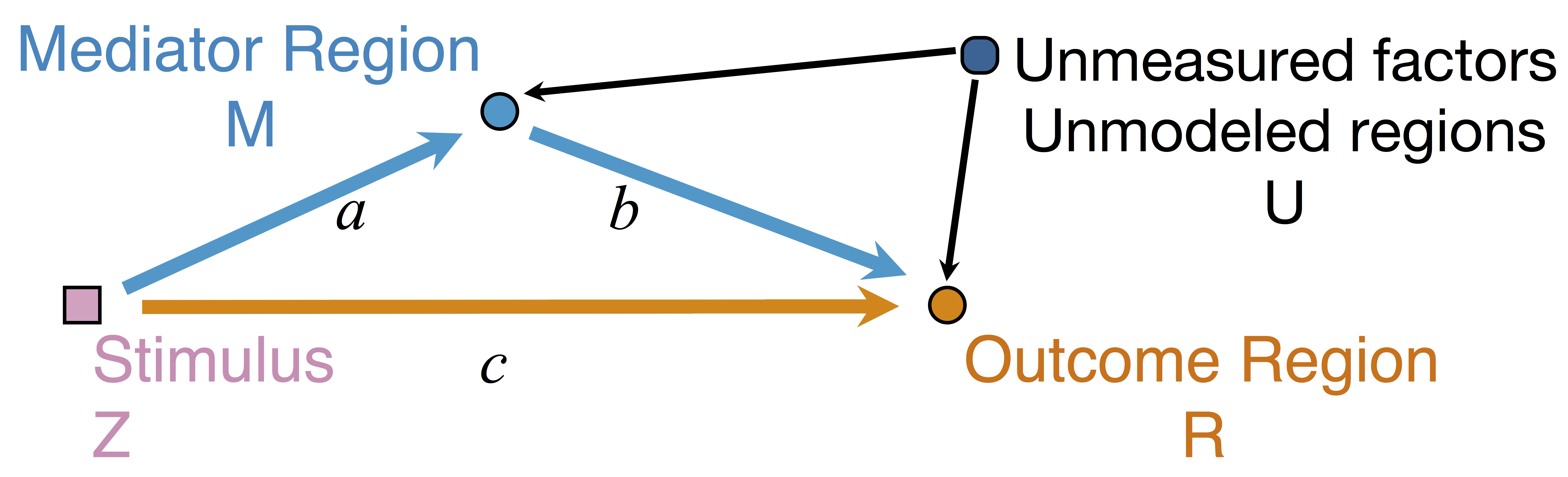$$\small \begin{align*}M &= Z a + \overbrace{U + \epsilon_1}^{E_1}\qquad R = Z c + M b + \underbrace{U g + \epsilon_2}_{E_2}, \quad \epsilon_1 \bot \epsilon_2\end{align*}$$
  • Indirect effect: $a \times b$; Direct effect: $c$
  • Untestable assumption: $\delta=cor(E_1, E_2) =0 $, no confounders Baron&Kenny, 86; Sobel, 82; Holland 88; Preacher&Hayes 08; Imai et al, 10; VanderWeele, 15; Lindquist, 12 ...

We first prove two different models generate same single-trial BOLD activations if only observing $Z$, $M$, and $R$

without measuring $U$

Multilevel Mediation Zhao and Luo, 2023

  • We optimize the joint likelihood of all multilevel mediation data, allowing $\delta \ne 0$
  • We prove a unique solution and consistent estimation for $\delta$.
  • From data alone, we estimate the causal effects, without the untestable assumption of no unmeasured confounding.
  • Large fMRI data is helpful for resolving causality

Model Identifiability and Bias

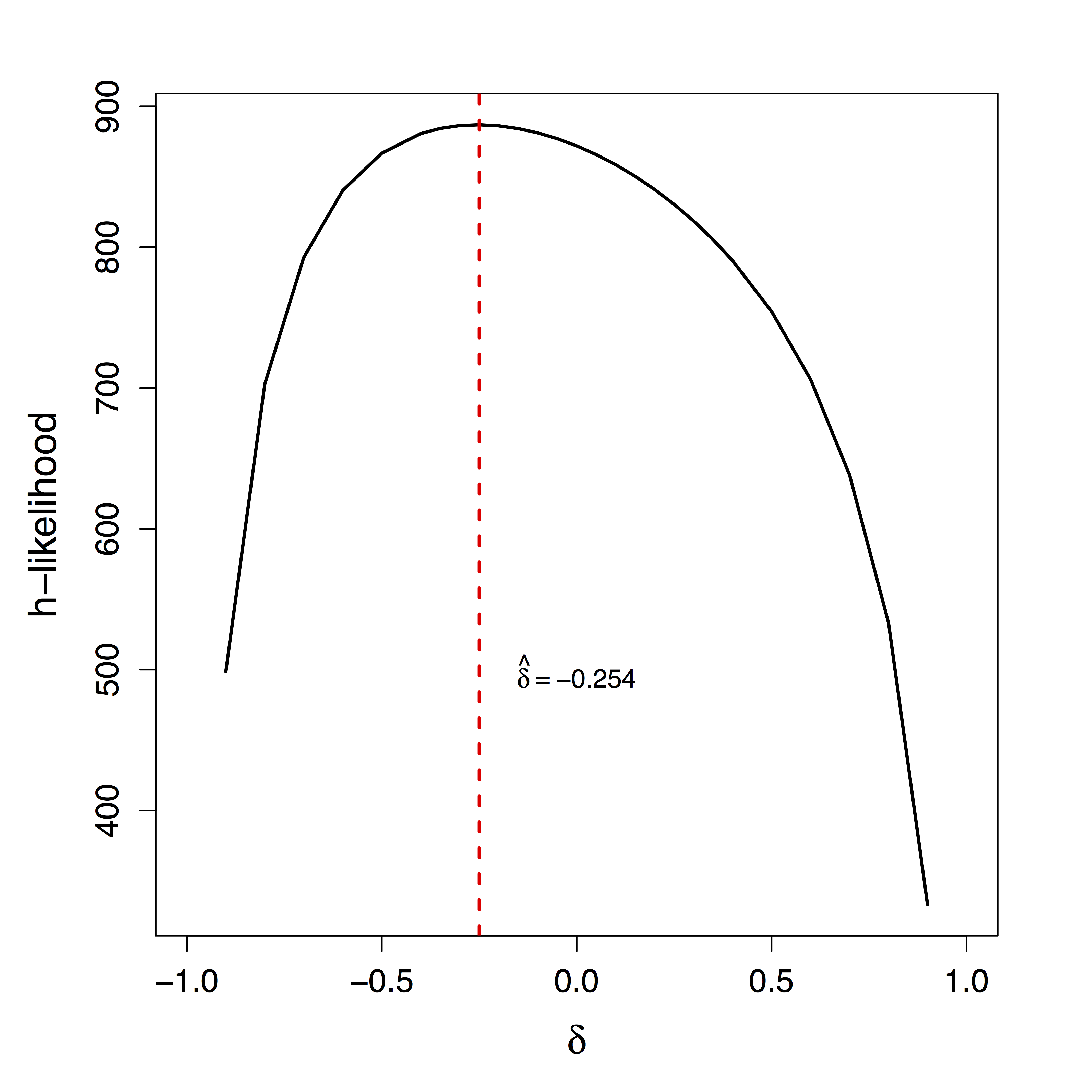
Unique $\delta$ for ML

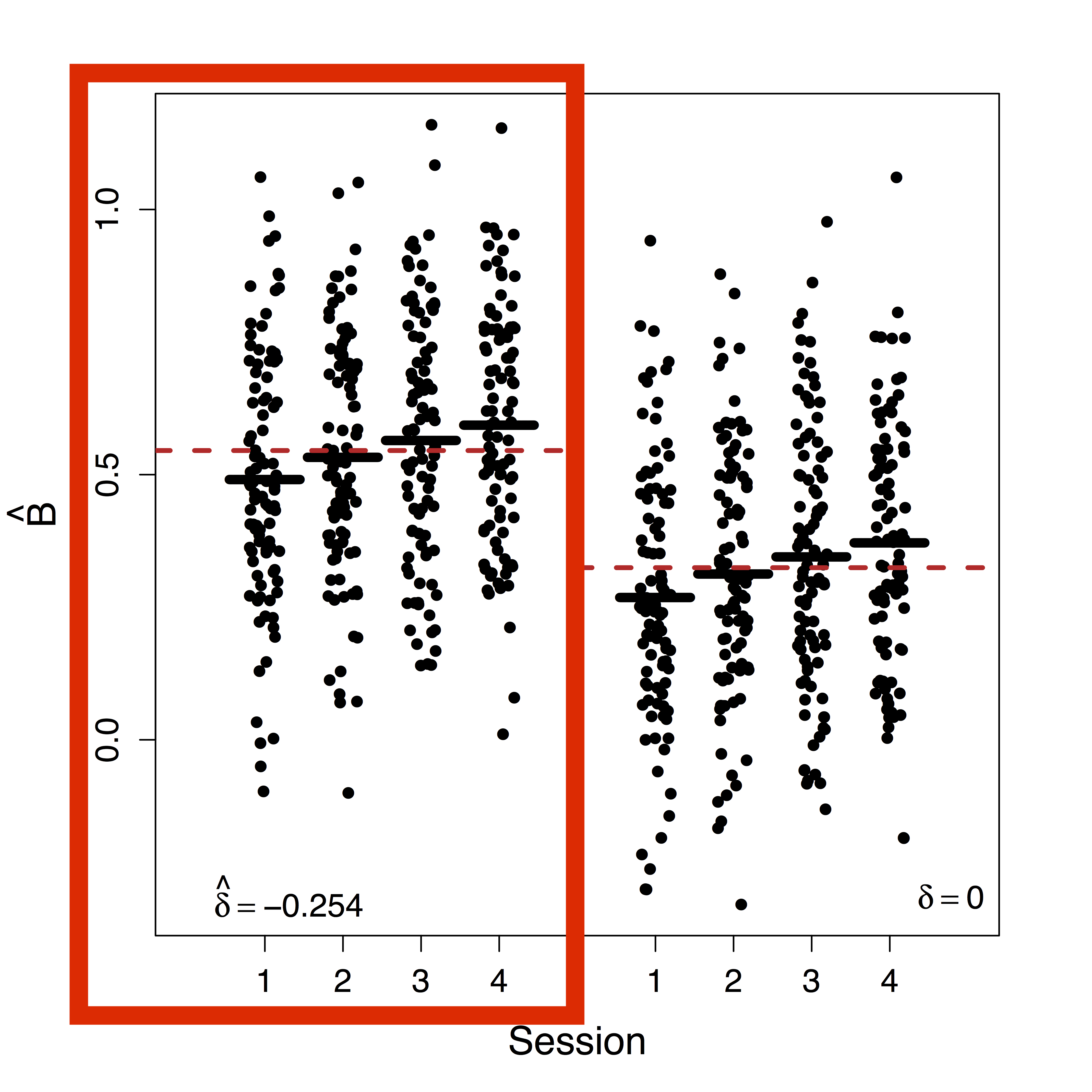
Effects doubled


Causal effects in fMRI actually larger after removing unmeasured confounding

Granger Mediation Zhao and Luo, 2019

  • We build multilevel, time series mediation model, based on Granger causality or VAR
  • A spatial-temporal model for brain pathways
  • We specify additional causal assumptions
  • We prove asymptotic convergence rates

Granger Mediation Model


→ Time

Simulations Match Theory

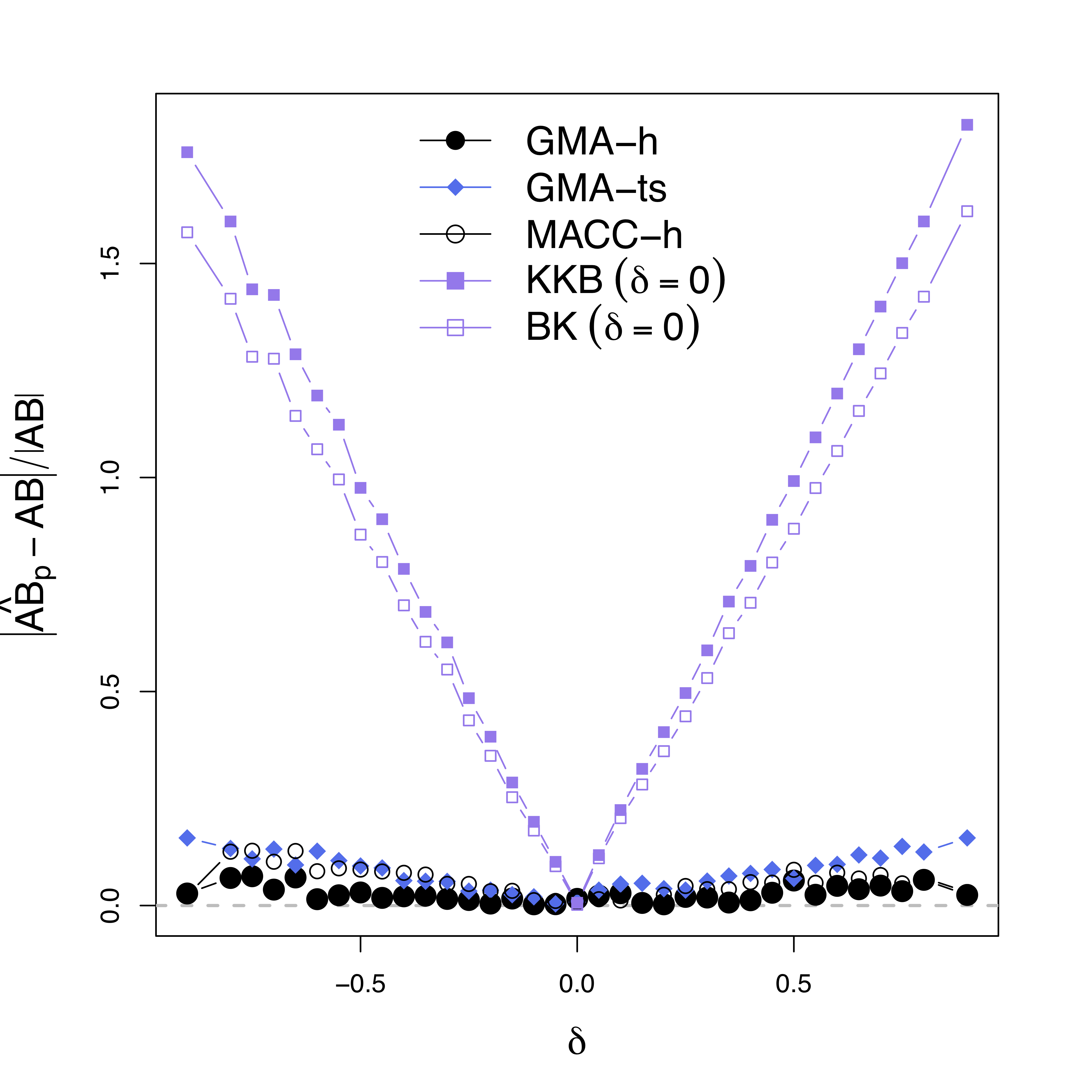
Low bias for $AB$

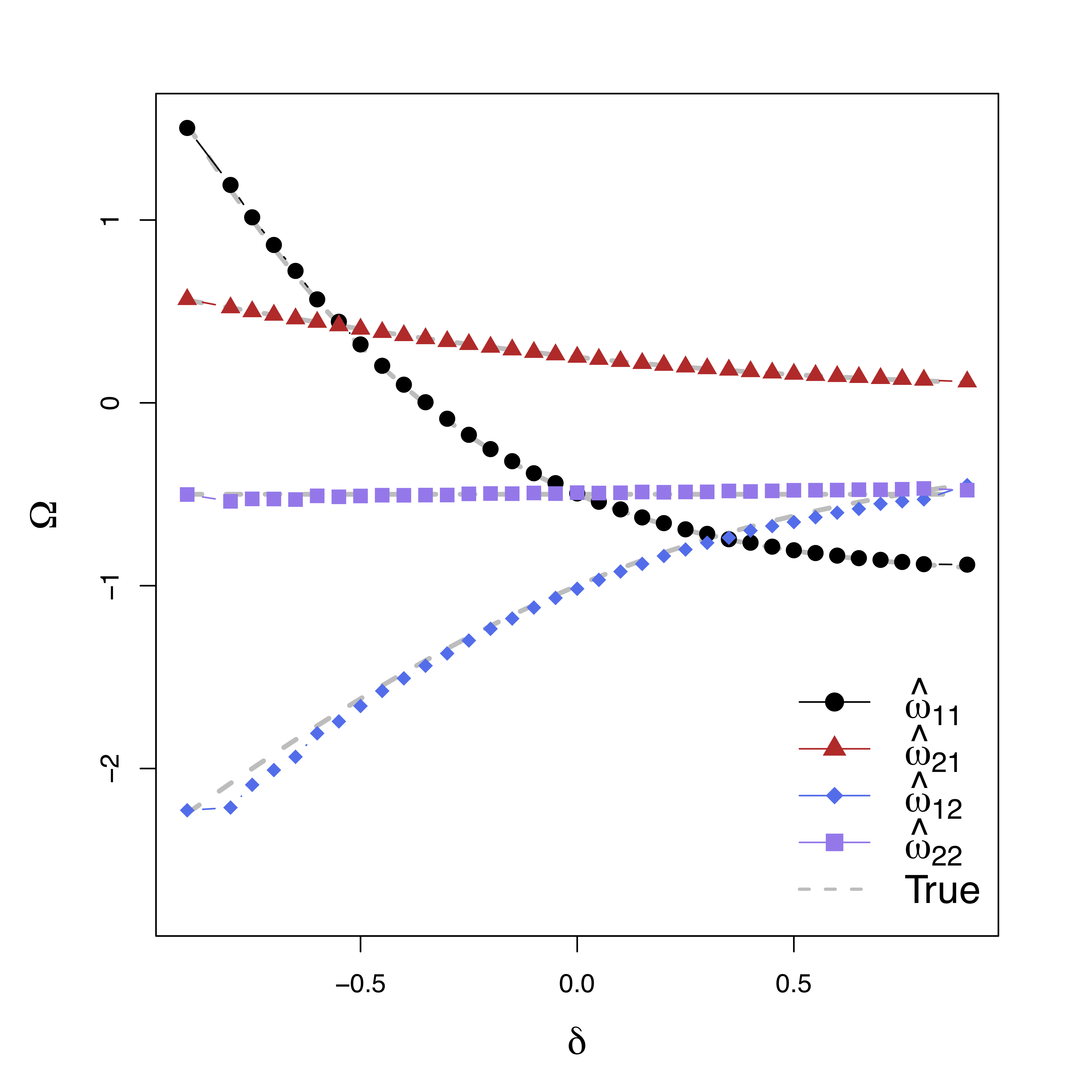
Low bias for temporal cor

Gray dash lines are the truth

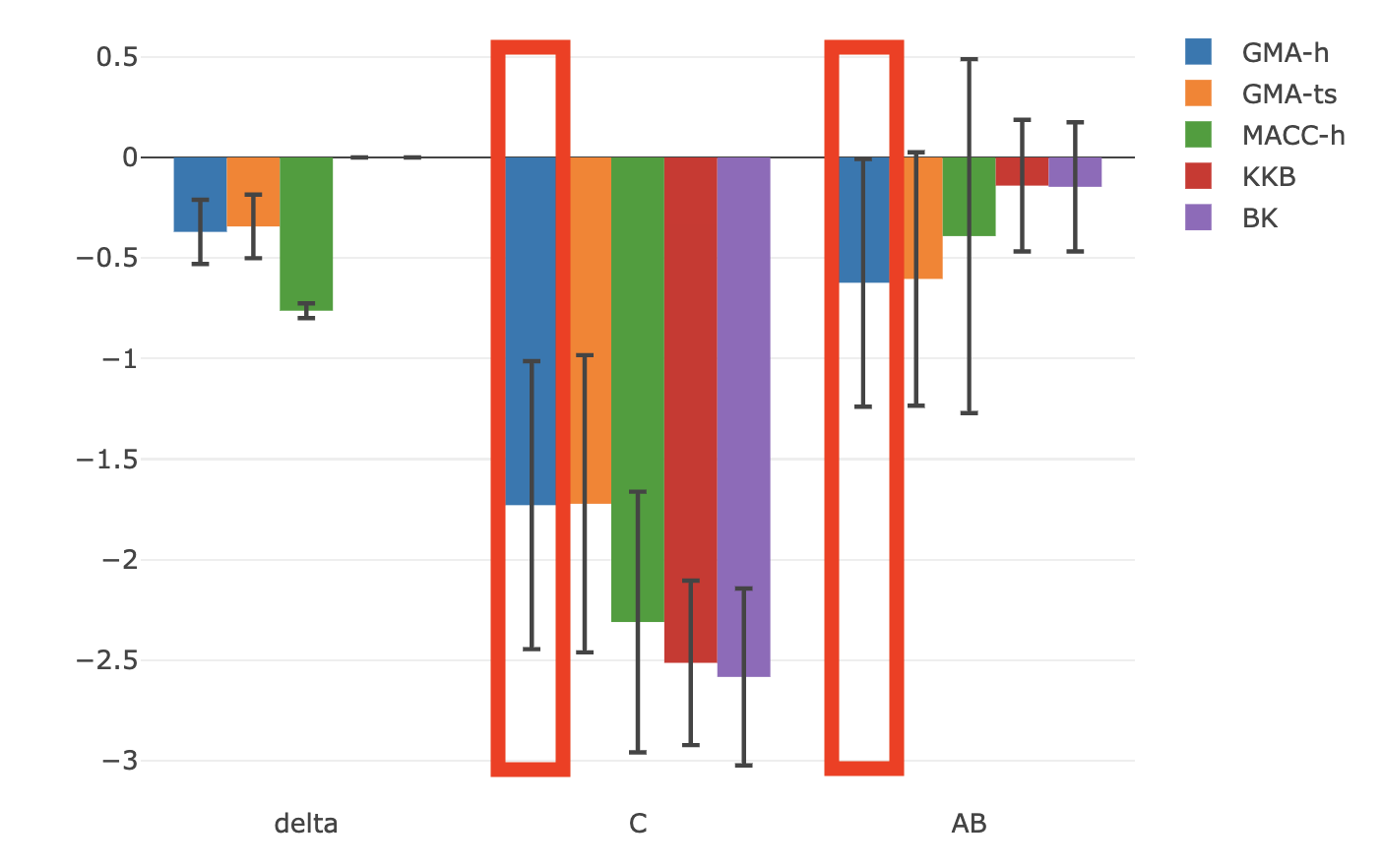
GMA performs the best, and recovers the temporal correlations

  • Stronger indirect pathways while other methods under-estimate the effects/ratios
    • Help resolve the debates among neuroscientists
  • Novel feedback findings: M1 → preSMA after lag 1 and 2 (not shown)

Functional Mediation Zhao, Luo, Sobel, Lindquist, Caffo, arXiv

  • We treat all variables as functional data
  • We identify the causal assumptions necessary for causal interpretation
  • Improved understanding of dynamic mediation effects and interpretation

Historical Model: Direct and Indirect Effects

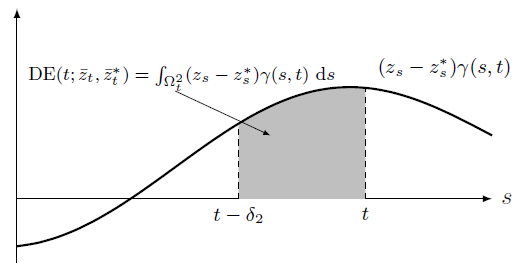
Direct Effect

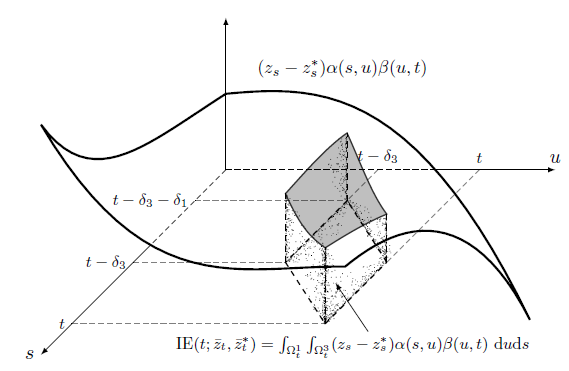
Indirect Effect



Causal effects are 1D/2D integration of the shaded

Causal SEMs: Historical Model

$$ \scriptsize \begin{align} M_{t}(\bar{z}_{t}) =& \iota_{1}(t)+ \int_{\Omega_{t}^{1}}z_{s}\alpha(s,t)~\mathrm{d}s+\varepsilon_{1t}(\bar{z}_{t}), \label{eq:CHM_M} \\ Y_{t}(\bar{z}_{t},\bar{m}_{t}) =& \iota_{2}(t) + \int_{\Omega_{t}^{2}}z_{s}\gamma(s,t)~\mathrm{d}s \\ & +\int_{\Omega_{t}^{3}}m_{s}\beta(s,t)~\mathrm{d}s+\varepsilon_{2t}(\bar{z}_{t},\bar{m}_{t}) \label{eq:CHM_Y} \end{align} $$
Theorem. Under the assumptions and the above models, $\mathrm{TE}(t;\bar{z}_{t},\bar{z}_{t}^{*})$ is parametrically identified: $$ \begin{align} \scriptsize \int_{\Omega_{t}^{2}}(z_{s}-z_{s}^{*})\gamma(s,t)~\mathrm{d}s+\int_{\Omega_{t}^{1}}(z_{s}-z_{s}^{*})\int_{\Omega_{t}^{3}}\alpha(s,u)\beta(u,t)~\mathrm{d}u~\mathrm{d}s. \end{align} $$ and the direct and indirect components are also parametrically identified.

Simulation Comparison

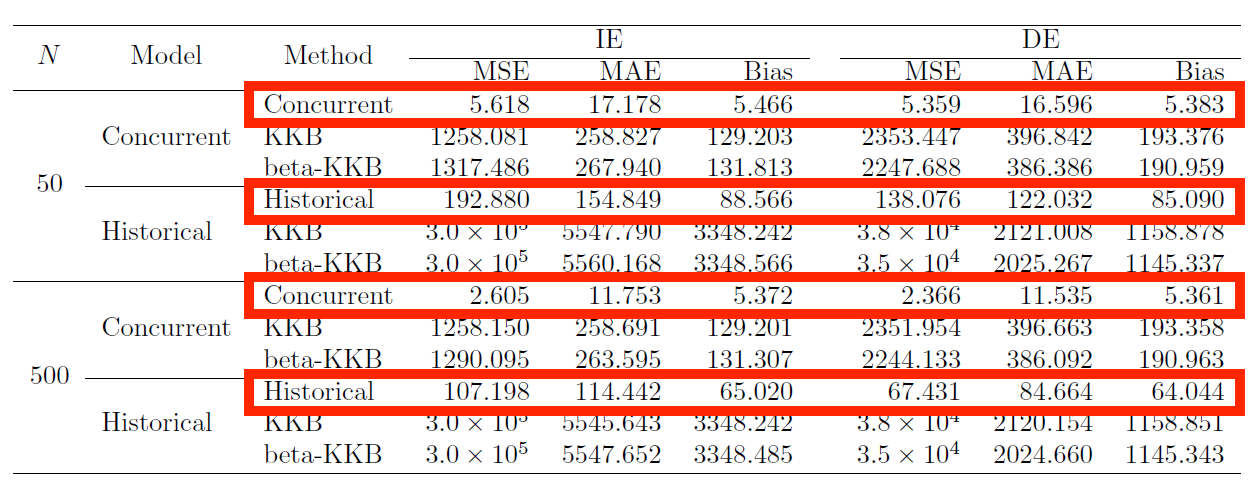
Challenging for scalar mediation methods to capture functional causal effects

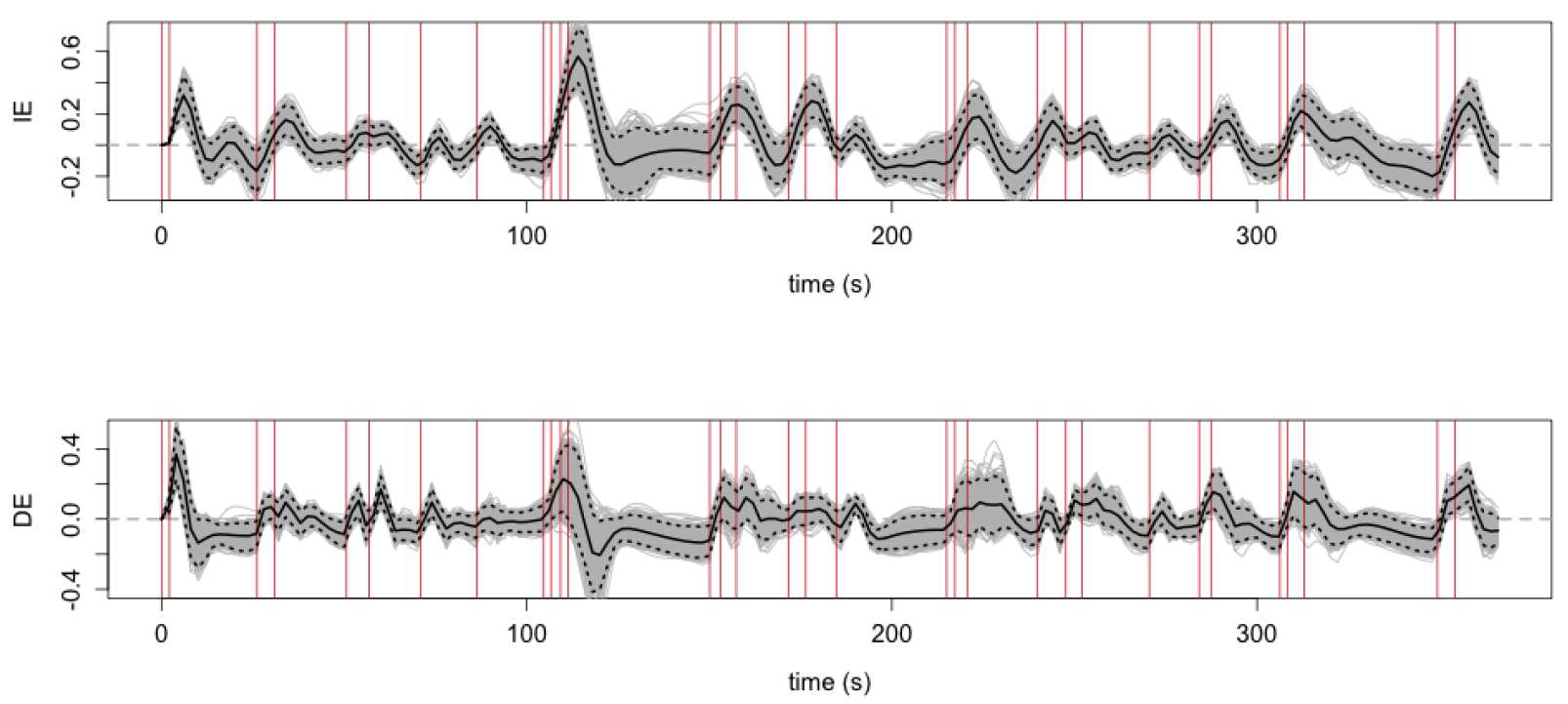
Brain mediation effects are dynamic depending on stimulus patterns and history

High Dim Mediation Zhao and Luo, 2022

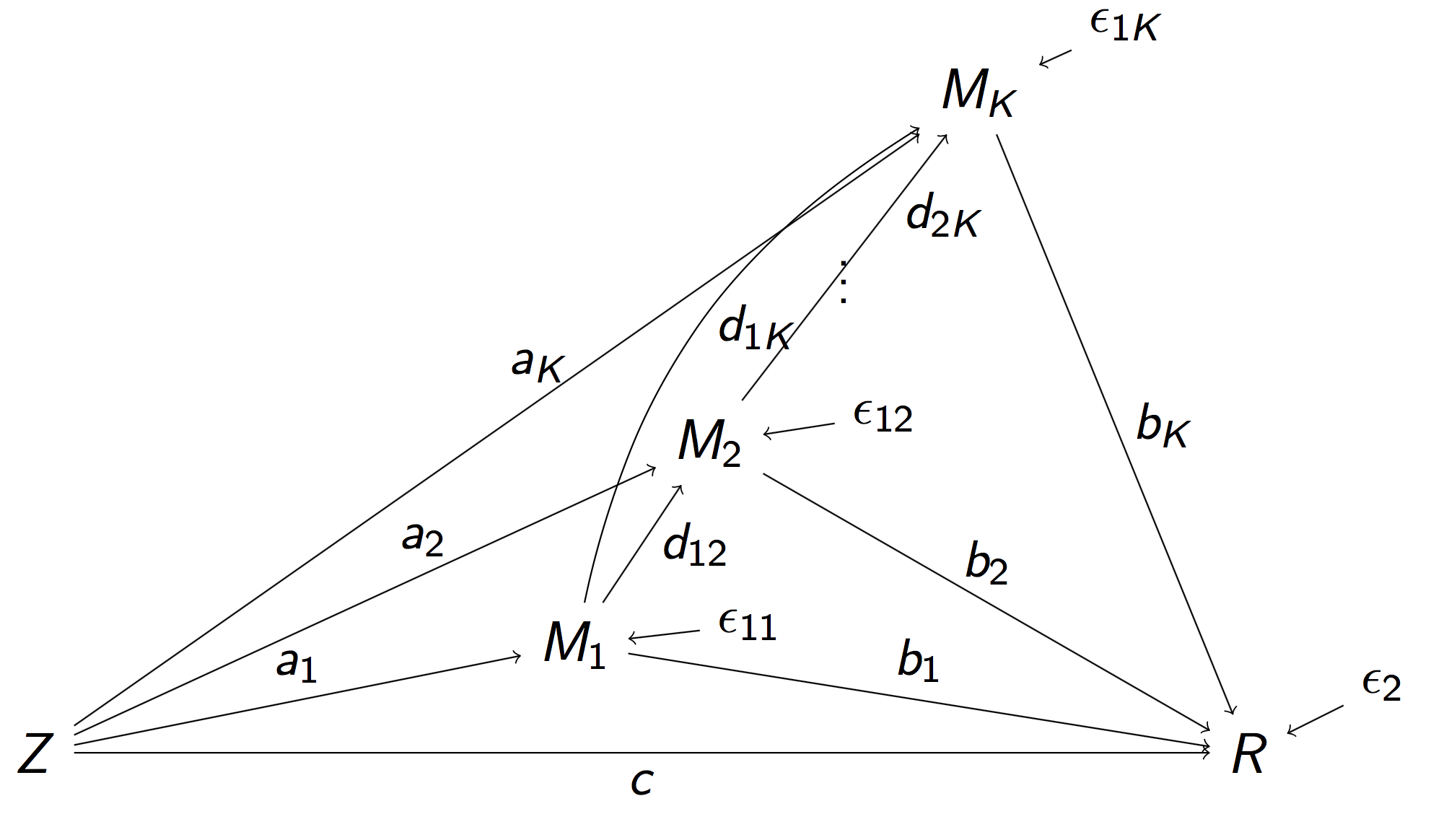
Full Model

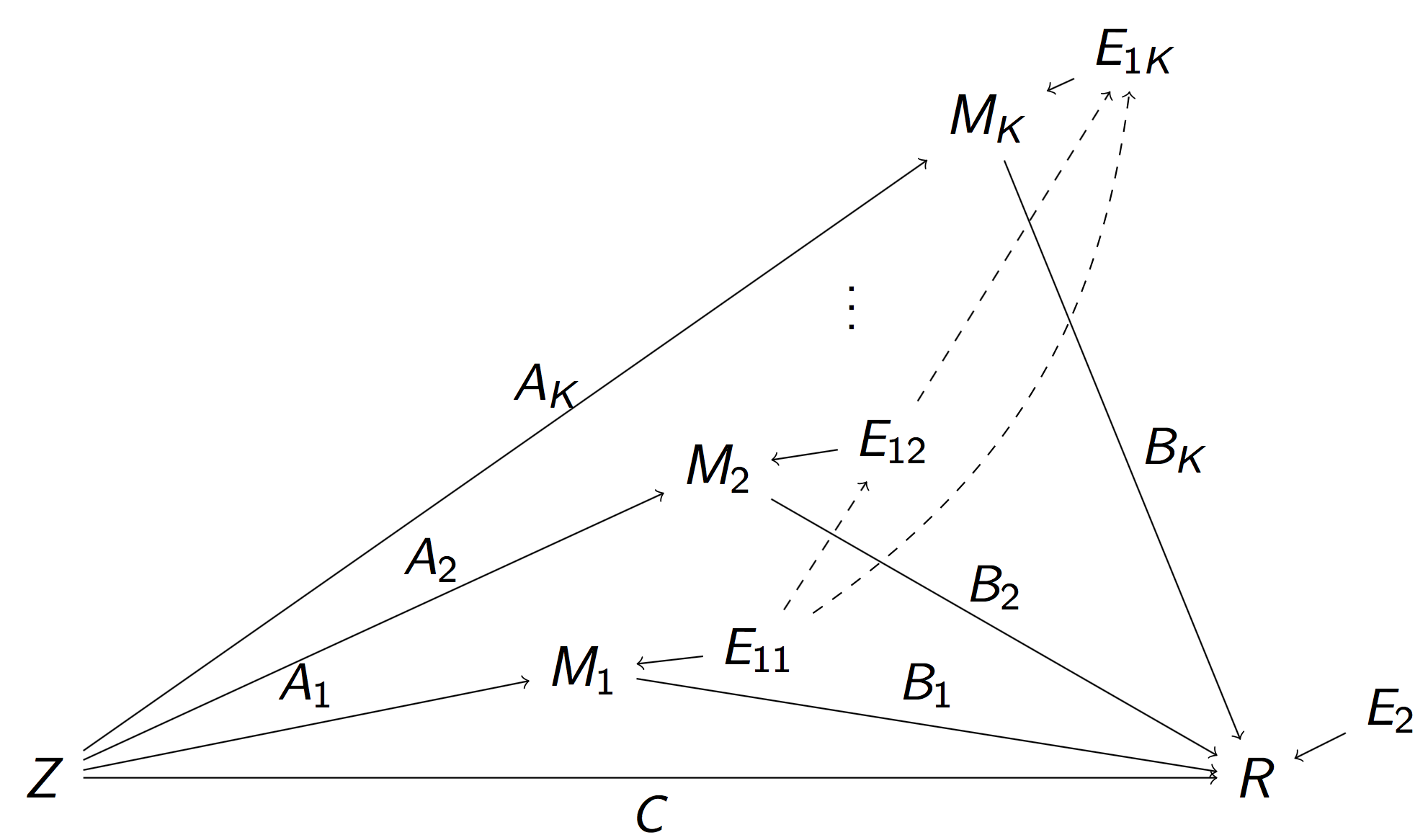
Reduced Model

$$\scriptsize \sum_{k=1}^K \| M_k - Z A_k \|_2^2 + \| R - Z C - \sum_k M_k B_k \|_2^2 + \mbox{Pen}(A, B)$$

Pathway Lasso penalty:

$$ \scriptsize \mbox{Pen}(A, B) = \lambda \sum_{k=1}^K ( |A_k B_k| + \phi A_k^2 + \phi B_k^2) $$

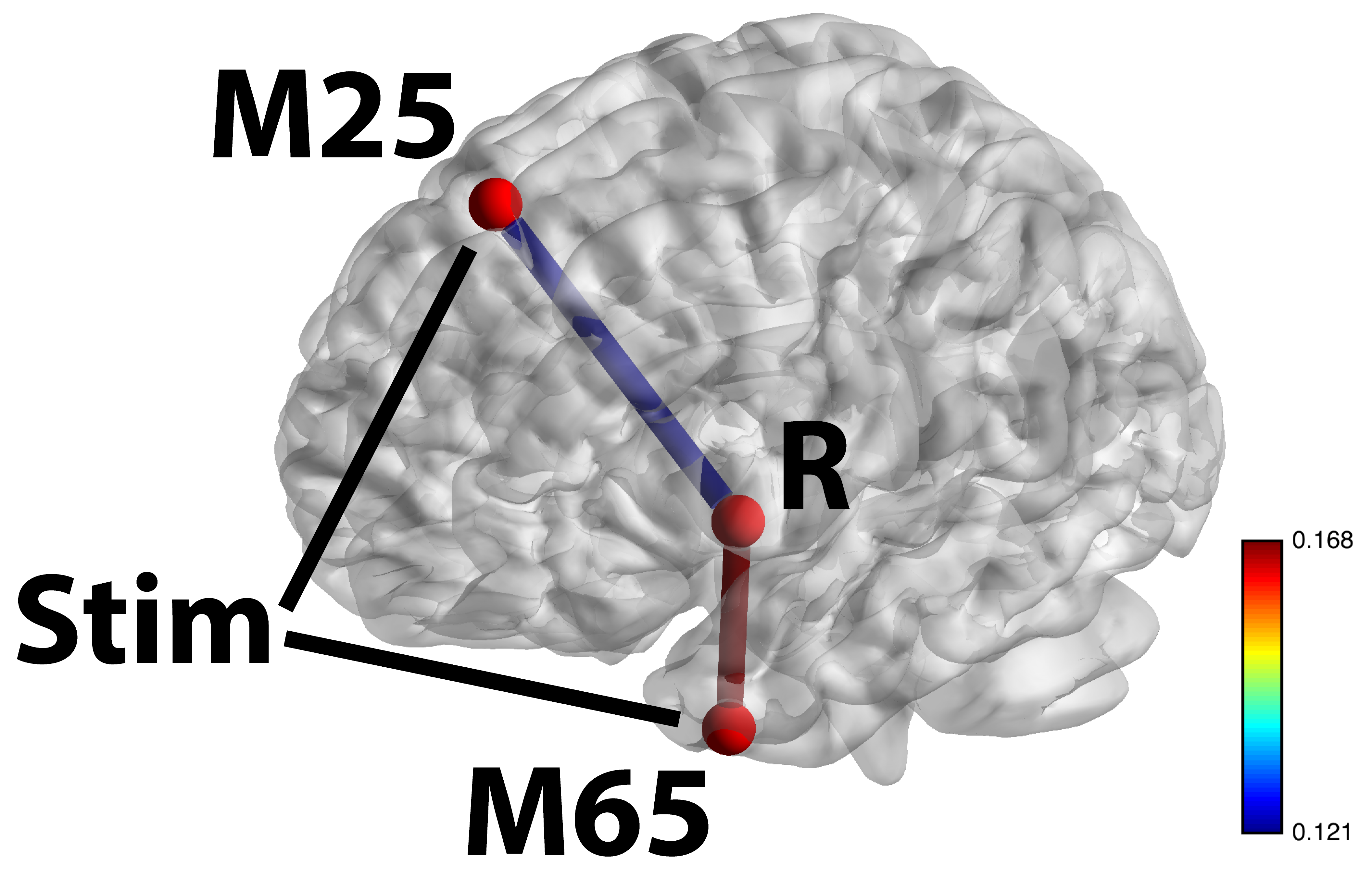
Stim-M25-R and Stim-M65-R significant shown largest weight areas

  • M65 responsible for language processing, larger flow under story
  • M25 responsible for uncertainty, larger flow under math

Summary

  • Causal mediation analysis for fMRI can improve effect estimates
  • Multilevel and large-scale models help resolve causality (a bit), under varying statistical and causal assumptions
  • Mediation can be useful for understanding brain pathways and information processing
  • R packages available: macc, gma, cfma and references within

Collaborators

Yi Zhao

Yi Zhao
Indiana Univ

Michael Sobel

Michael Sobel
Columbia Univ

Martin Lindquist

Martin Lindquist
Johns Hopkins Univ

Brian Caffo

Brian Caffo
Johns Hopkins Univ

Important Questions

  1. Important research problems?
    • Validation, large-scale joint causal models, directionality, to bedside
  2. How to improve the processing and sharing of datasets?
    • Benchmark datasets
  3. How to make statistical methods more impactful?
    • Integration with the ecosystem, case studies, scientific meetings