Network Clustering with an Application to fMRI
Xi (Rossi) LUO
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science
Brown Data Science Initiative
ABCD Research Group

June 16, 2017
Funding: NSF/DMS (BD2K) 1557467; NIH R01EB022911, P20GM103645, P01AA019072, P30AI042853
Collaborators

Florentina Bunea
Cornell University

Christophe Giraud
Paris Sud University
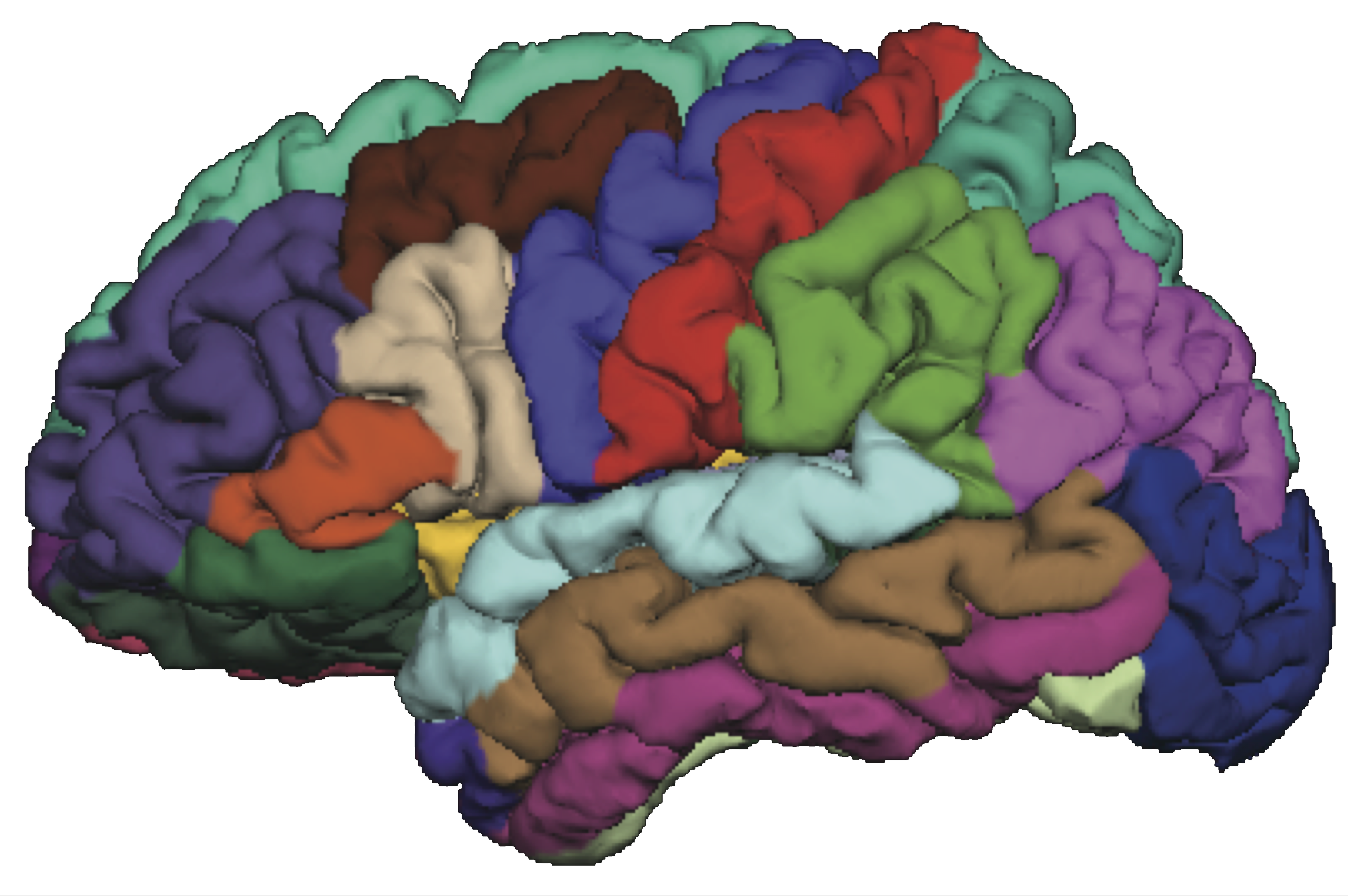
Task fMRI
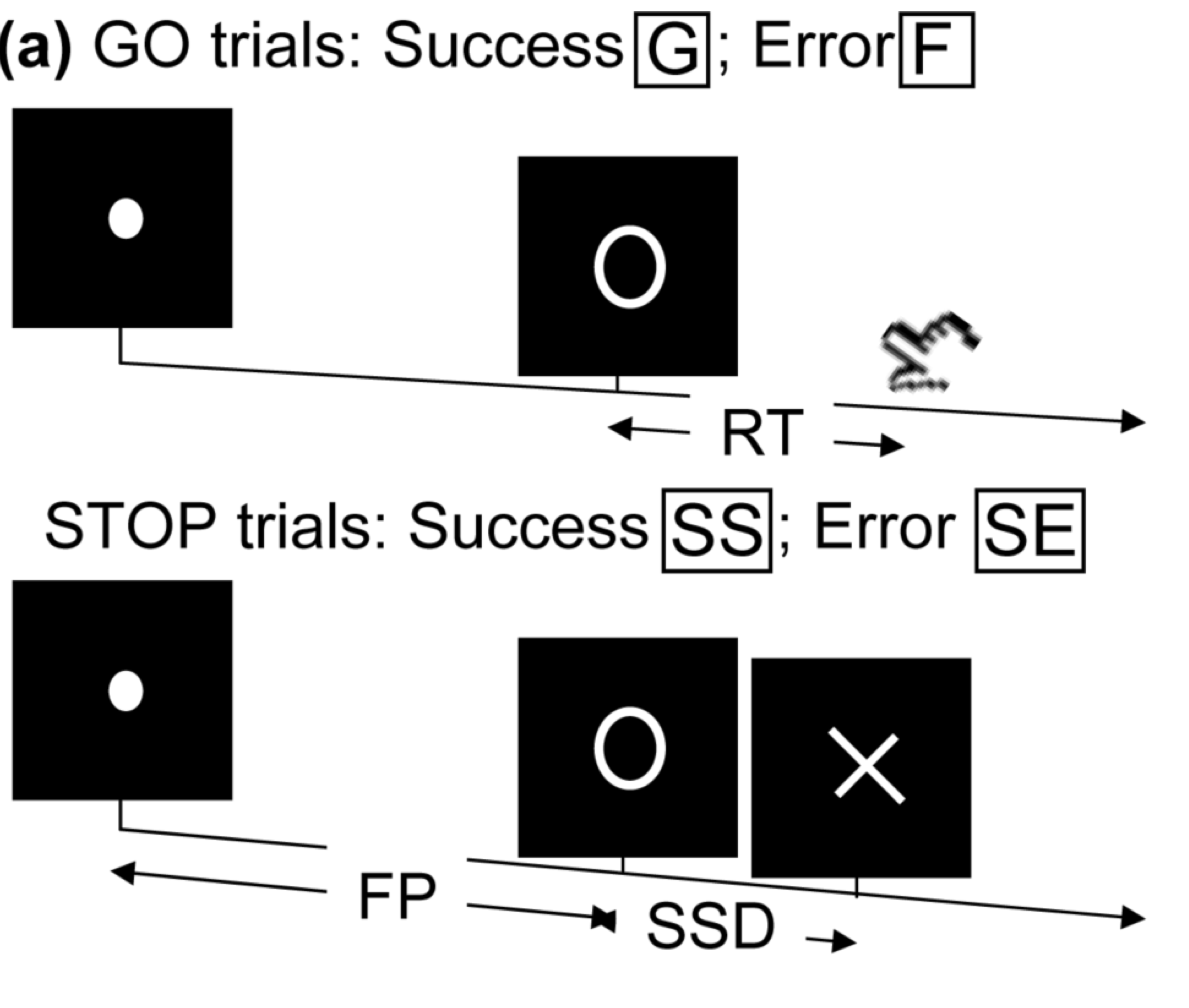
- Perform tasks while under fMRI scanning
- Specific parts of the brain responsible for the task
- Remove task effects, data like "resting-state"
fMRI data: blood-oxygen-level dependent (BOLD) signals from each
Data Matrix
- Matrix $X_{n \times p}$, all columns standardized
- $n$ time points but temporal correlation removed, like iid
- $p$ voxels but with spatial corraltion
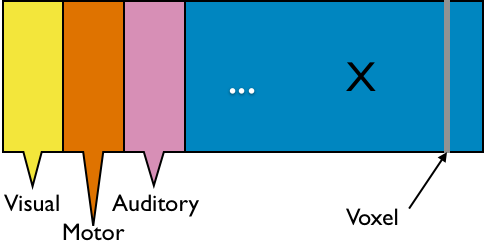
- Interested in
big spatial networks- Voxel level: $10^6 \times 10^6$ cov matrix but limited interpretability
"Network of Networks"
- Hierarchical Covariance Model (a latent var model)
- Some ongoing research related to this model
- How to cluster variables together?
- How to estimate cluster signals?
- How to estimate between-cluster connections?
- ...
- Will focus on how to group nodes together today
- Usually NP-hard and limited theory
Big Picture
- We are interested in
big cov with many variables- Global property for certain joint distributions
- Real-world cov: maybe
non-sparse and other structures
- Clustering successful for > 40 years and for DSDonoho, 2015
- Exploratory Data Analysis (EDA)Tukey, 1977
- Hierarchical clustering and KmeansHartigan & Wong, 1979
- Usually based on marginal/pairwise distances
- Can clustering and big cov estimation be combined?
Example
Example: SP 100 Data
- Daily returns from stocks in SP 100
- Stocks listed in Standard & Poor 100 Indexas of March 21, 2014
- between January 1, 2006 to December 31, 2008
- Each stock is a variable
- Cov/Cor matrices (Pearson's or Kendall's tau)
-
Re-order stocks by clusters - Compare cov patterns with different clustering/ordering
-
Cor after Grouping by Clusters
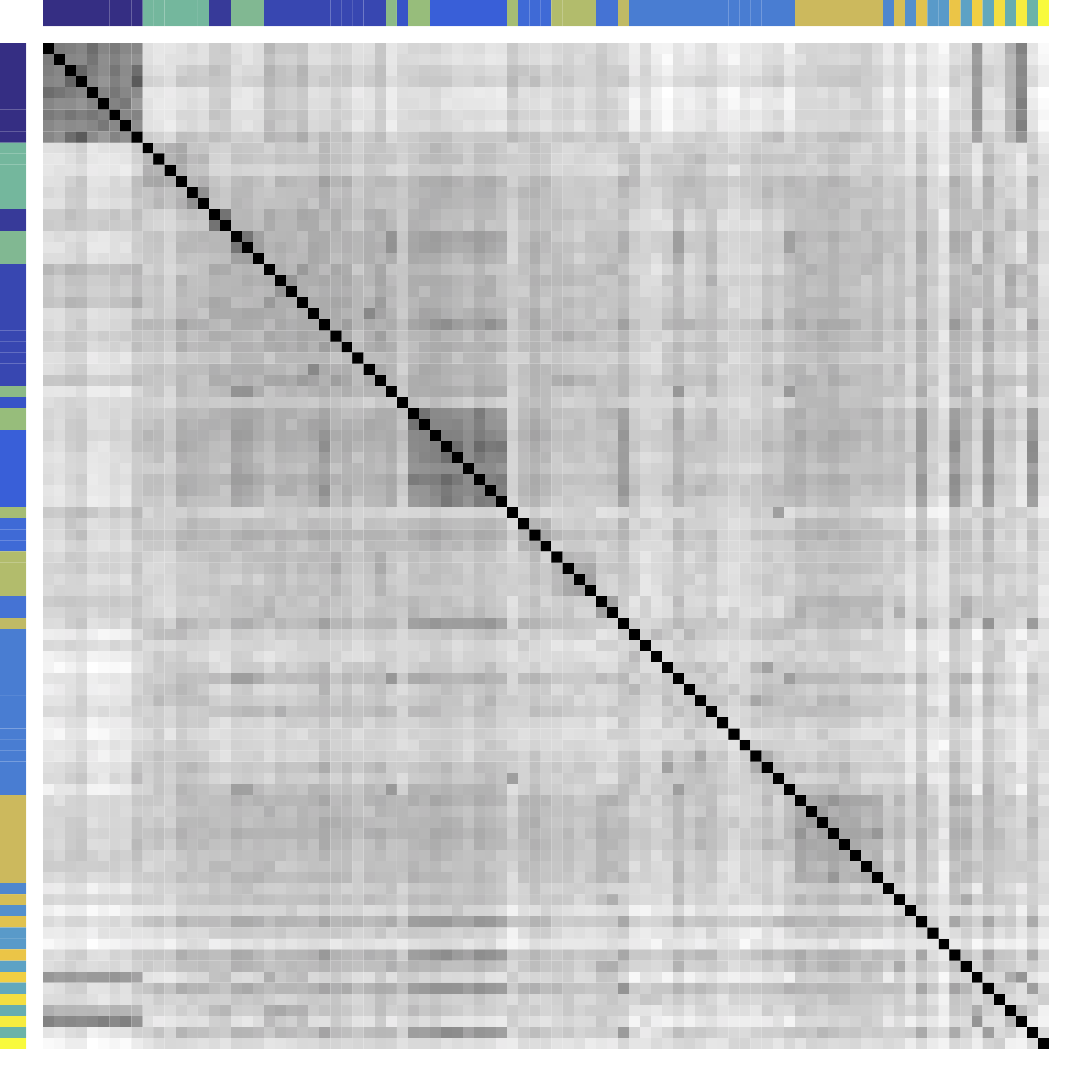

Ours yields stronger
Color bars: variable groups/clusters
Off-diagonal: correlations across clusters
Clustering Results
| Industry |
|
Kmeans | Hierarchical Clustering |
|---|---|---|---|
| Telecom | ATT, Verizon | ATT, Verizon, Pfizer, Merck, Lilly, Bristol-Myers | ATT, Verizon |
| Railroads | Norfolk Southern, Union Pacific | Norfolk Southern, Union Pacific | Norfolk Southern, Union Pacific, Du Pont, Dow, Monsanto |
| Home Improvement | Home Depot, Lowe’s | Home Depot, Lowe’s, Starbucks | Home Depot, Lowe’s, Starbucks, Costco, Target, Wal-Mart, FedEx, United Parcel Service |
| $\cdots$ | |||
Model
Problem
- Let ${X} \in \real^p$ be a zero mean random vector
- Divide variables into partitions/clusters
- Example: $\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$
- Theoretical: define
uniquely identifiable partition $G$ such that all $X_a$ in $G_k$ are statistically"similar" - DS: find
"helpful" partition that show cov patterns
Related Methods
- Clustering: Kmeans and hierarchical clustering
- Advantages: fast, general, popular
- Limitations: low signal-noise-ratio, theory
- Community detection: huge literature see review Newman, 2003 but start with observed
adjacency matrices
Kmeans
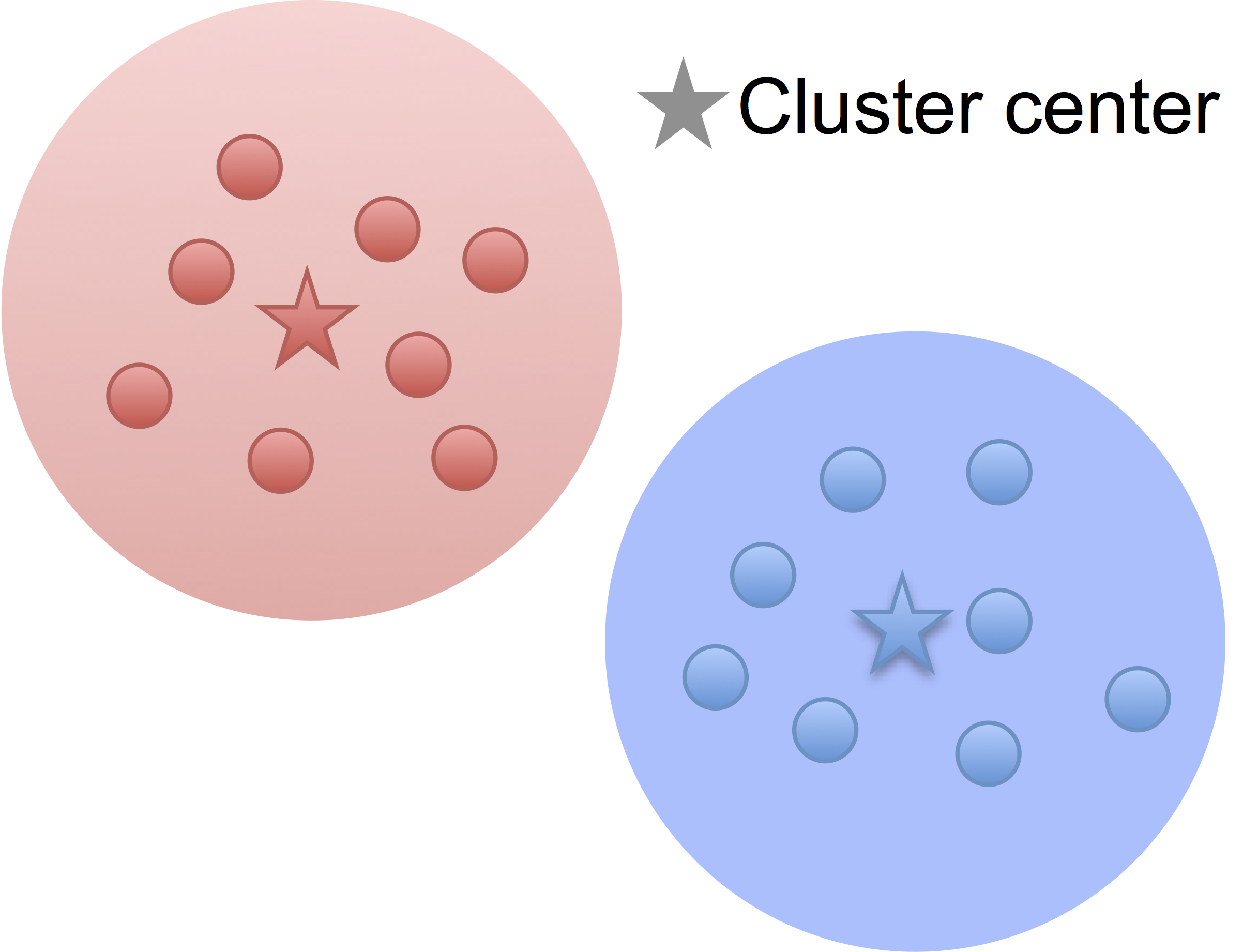
Low noise
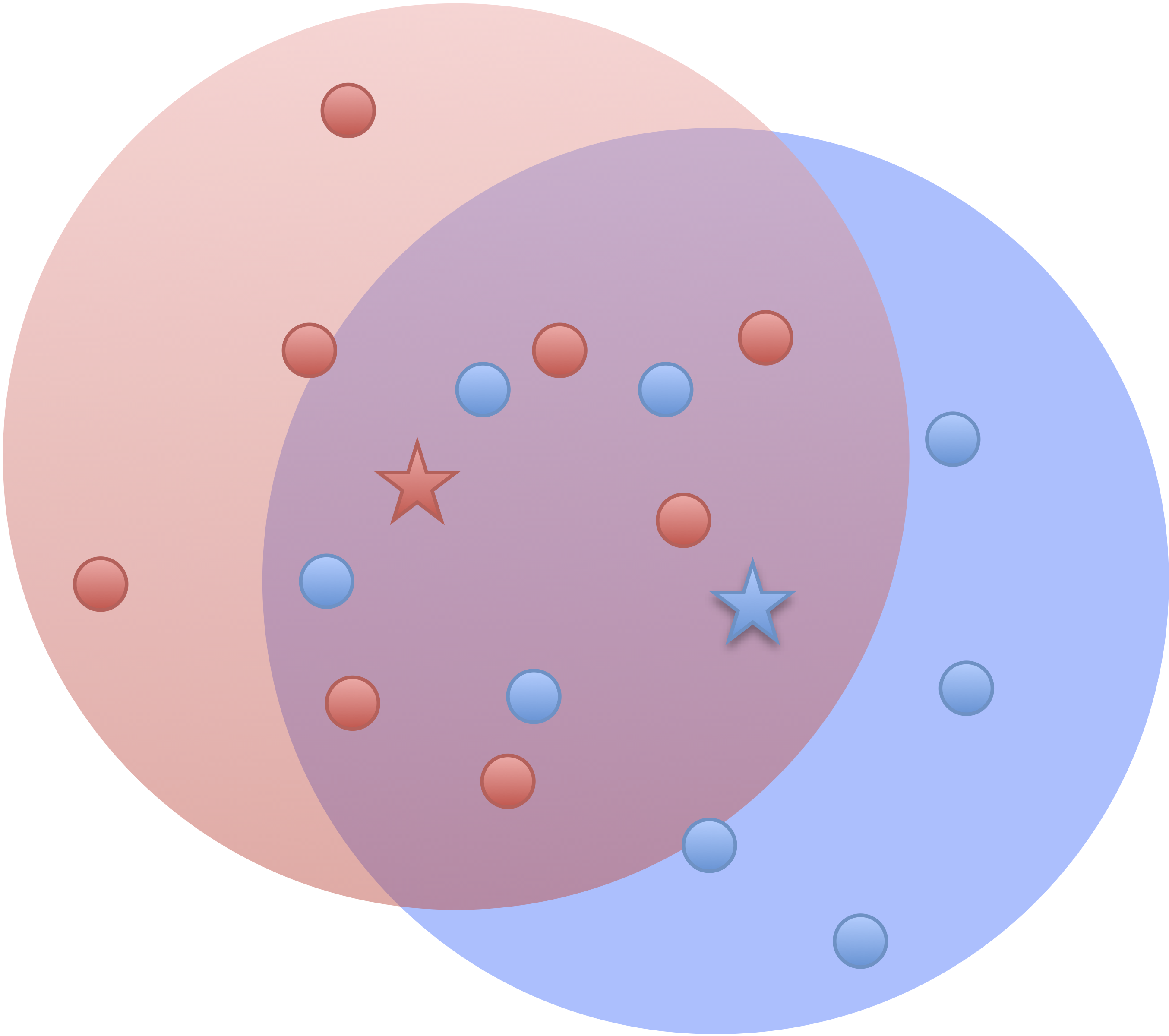
High noise
- Cluster points together if pairwise distance small
- Clustering accuracy
depends on the noise
Kmeans: Generative Model
- Data $X_{n\times p}$: $p$ variables from partition $G$: $$G=\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$$
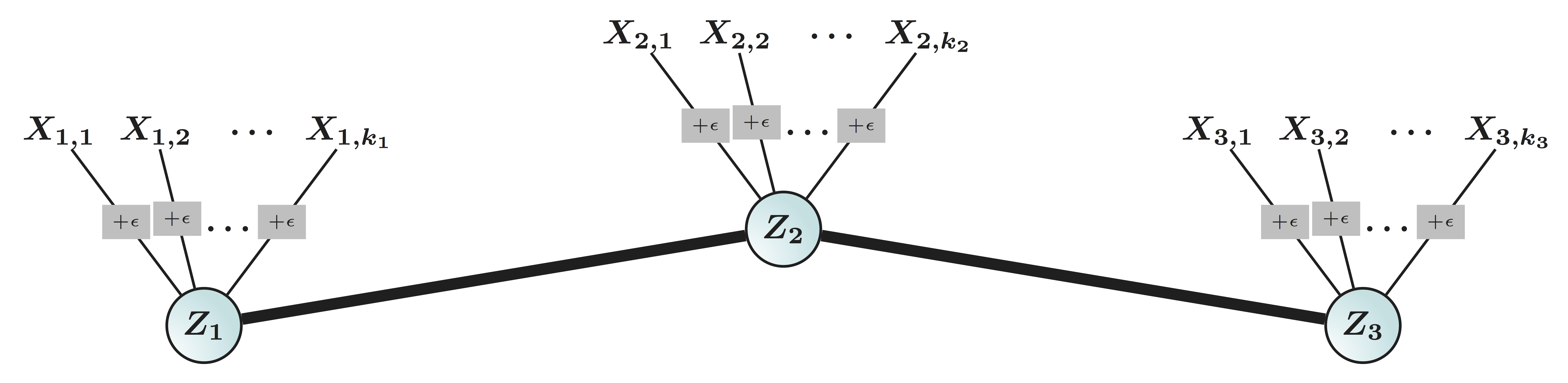
- Mixture Gaussian: if variable $X_j \in \real^n$ comes from cluster $G_k$ Hartigan, 1975 $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j $$
- Kmeans minimizes over $G$ (and centroid $Z$): $$\sum_{k=1}^K \sum_{j\in G_k} \left\| X_j - Z_k \right\|_2^2 $$
$G$-Latent Cov
- We call $G$-latent model: $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j \mbox{ and } j\in G_k $$
- WLOG, all variables are standardized
- Intuition: variables $j\in G_k$ form net communitiesLuo, 2014
Matrix Representation
$$ X_{n\times p}=\underbrace{Z_{n\times k}}_\text{Source/Factor} \quad \underbrace{G_{k\times p}}_\text{Mixing/Loading} + \underbrace{E_{n\times p}}_{Error} \qquad Z \bot E$$
- Clustering: $G$ is $0/1$ matrix for $k$ clusters/ROIs
- Decomposition: under
conditions - PCA/factor analysis: orthogonality
- ICA: orthogonality → independence
- matrix decomposition: e.g. non-negativity
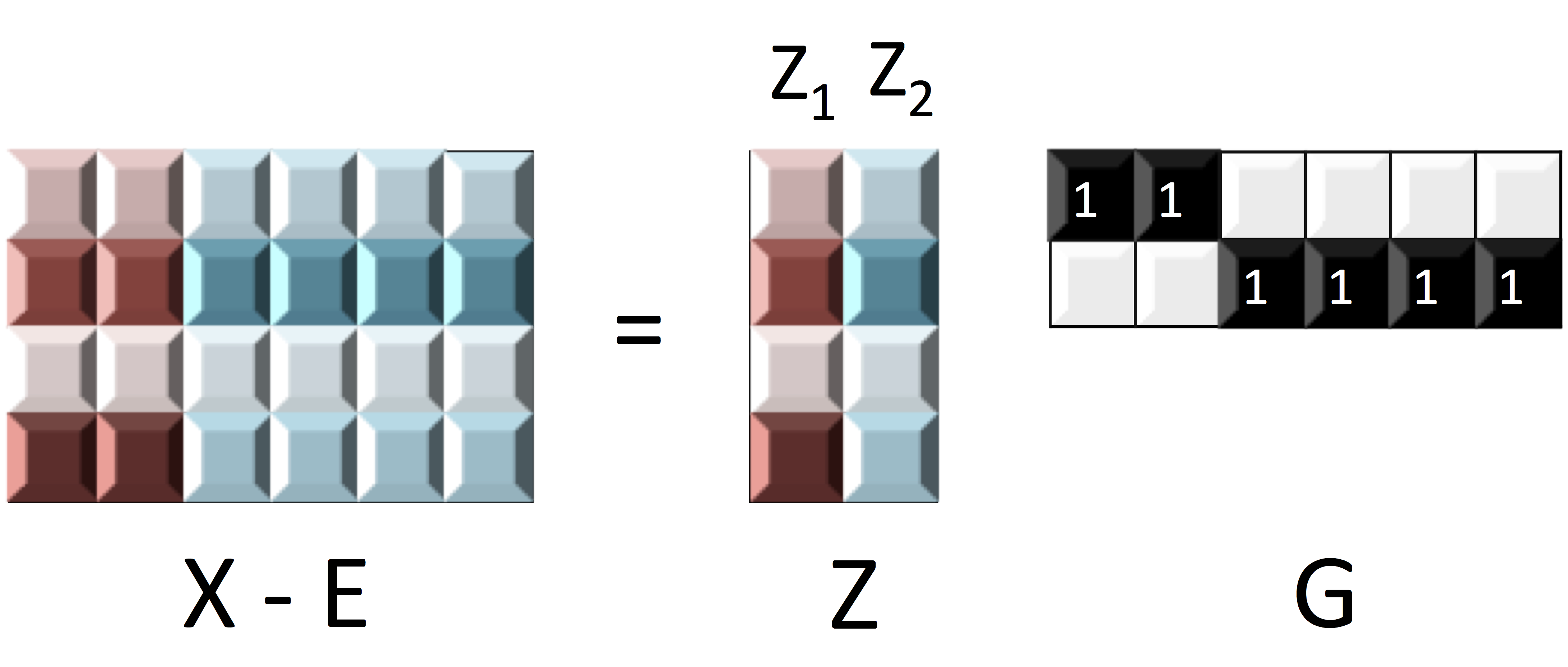
- Our model
identifiable if $\cor(Z_1, Z_2) \ne 0$- Two brain clusters red/blue talk to each other
- Identifiable if "$\cor(Z_1, Z_2) \gt \var(Z_1)\gt \var(Z_2)$"
- Other models
identifiable usually if $\cor(Z_1, Z_2) = 0$
Principals Behind Other Clustering
- The Euclidean distance for hierarchical clustering and Kmeans, for two columns/voxles $X_a$ and $X_b$: $$ \|X_a - X_b \|_2^2 = 2(1-\cor(X_a, X_b)) $$
- Recall $X_i = Z_k + E_i$ $i \in G_k$
- Cor depends
mainly on $\var(E)$ if SNR is low - Distance
- larger even if generated by same $Z$ and large error
- smaller even if generated by different $Z$ and small error
- Worse, clusters close because of correlated $Z$
Generalization
Example: $G$-Block
-
Set $G=\ac{\ac{1,2};\ac{3,4,5}}$, $X \in \real^p$ has $G$-block cov
$$\Sigma =\left(\begin{array}{ccccc} {\color{red} D_1} & {\color{red} C_{11} }&C_{12} & C_{12}& C_{12}\\ {\color{red} C_{11} }&{\color{red} D_1 }& C_{12} & C_{12}& C_{12} \\ C_{12} & C_{12} &{\color{green} D_{2}} & {\color{green} C_{22}}& {\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} D_2}&{\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} C_{22}}&{\color{green} D_2} \end{array}\right) $$ - Matrix math: $\Sigma = G^TCG + d$
- We allow $|C_{11} | \lt | C_{12} |$ or $C \prec 0$
- Kmeans/HC leads to block-diagonal cor matrices (permutation)
- Clustering based on $G$-Block
- Generalizing $G$-Latent which requires $C\succ 0$
Minimum $G$ Partition
Method
New Metric:
CORD
- First, pairwise correlation distance (like Kmeans)
- Gaussian copula: $$Y:=(h_1(X_1),\dotsc,h_p(X_p)) \sim N(0,R)$$
- Let $R$ be the correlation matrix
- Gaussian: Pearson's
- Gaussian copula: Kendall's tau transformed, $R_{ab} = \sin (\frac{\pi}{2}\tau_{ab})$
- Second, maximum difference of correlation distances $$\d(a,b) := \max_{c\neq a,b}|R_{ac}-R_{bc}|$$
- Third, group variables $a$, $b$ together if $\d(a,b) = 0$
The enemy of my enemy is my friend!
Image credit: http://sutherland-careers.com/
Algorithm: Main Idea
- Greedy: one cluster at a time, avoiding NP-hard
- Cluster variables together if CORD metric $$ \max_{c\neq a,b}|\hat{R}_{ac}-\hat{R}_{bc}| \lt \alpha$$ where $\alpha$ is a tuning parameter
- $\alpha$ is chosen by theory or CV
Theory
Condition
Consistency
Minimax
Choosing Number of Clusters
- Split data into 3 parts
- Use part 1 of data to estimate clusters $\hat{G}$ for each $\alpha$
- Use part 2 to compute between variable difference $$ \delta^{(2)}_{ab} = R_{ac}^{(2)} - R_{bc}^{(2)}, \quad c \ne a, b. $$
- Use part 3 to generate "CV" loss $$ \mbox{CV}(\hat{G}) = \sum_{a \lt b} \| \delta^{(3)}_{ab} - \delta^{(2)}_{ab} 1\{ a \mbox{ not clustered w/ } b \} \|^2_\infty. $$
- Pick $\alpha$ with the smallest loss above
Theory for CV
Simulations
Setup
- Generate from various $C$: block, sparse, negative
- Compare:
- Exact recovery of groups (theoretical tuning parameter)
- Cross validation (data-driven tuning parameter)
- Cord metric vs (semi)parametetric cor (regardless of tuning)
Exact Recovery
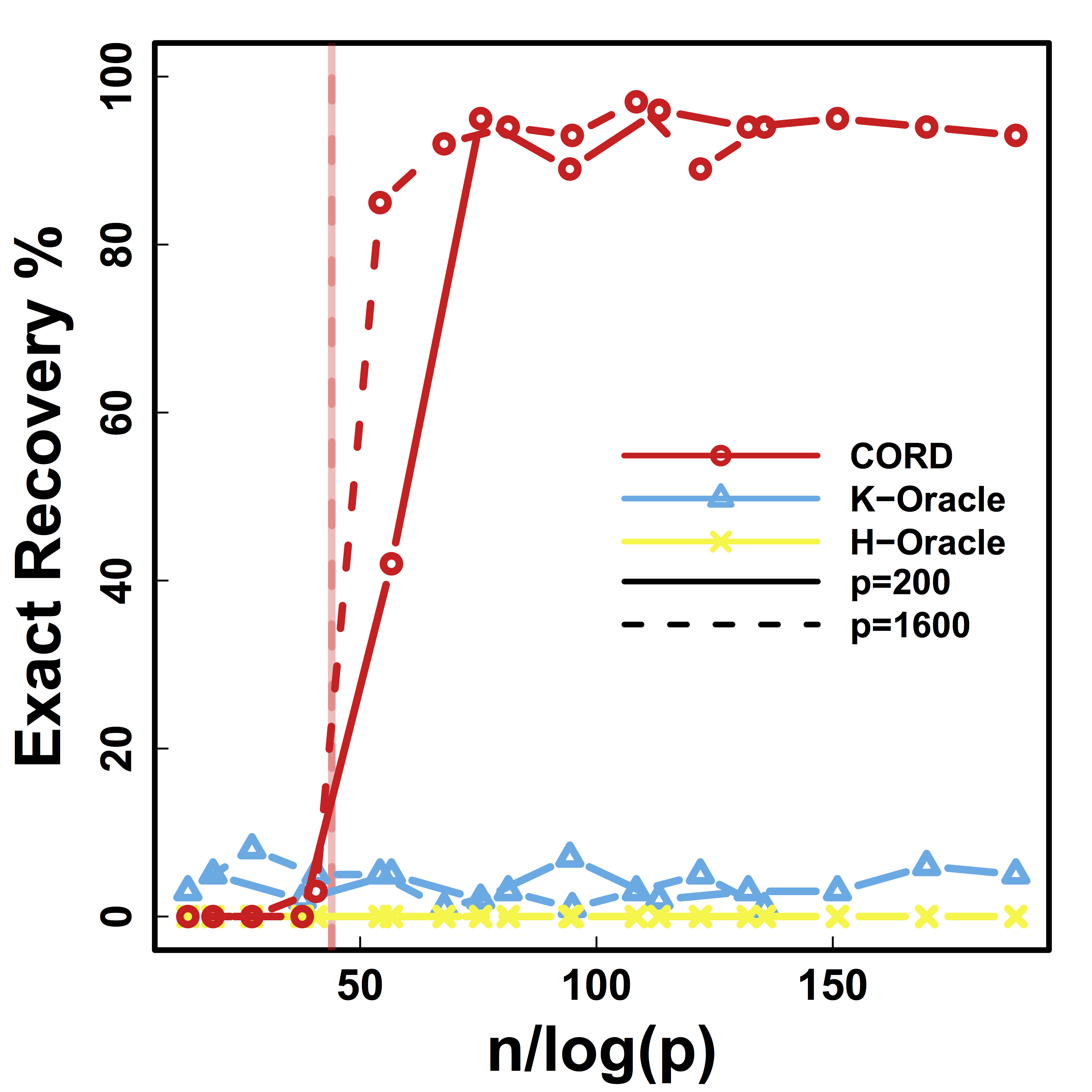
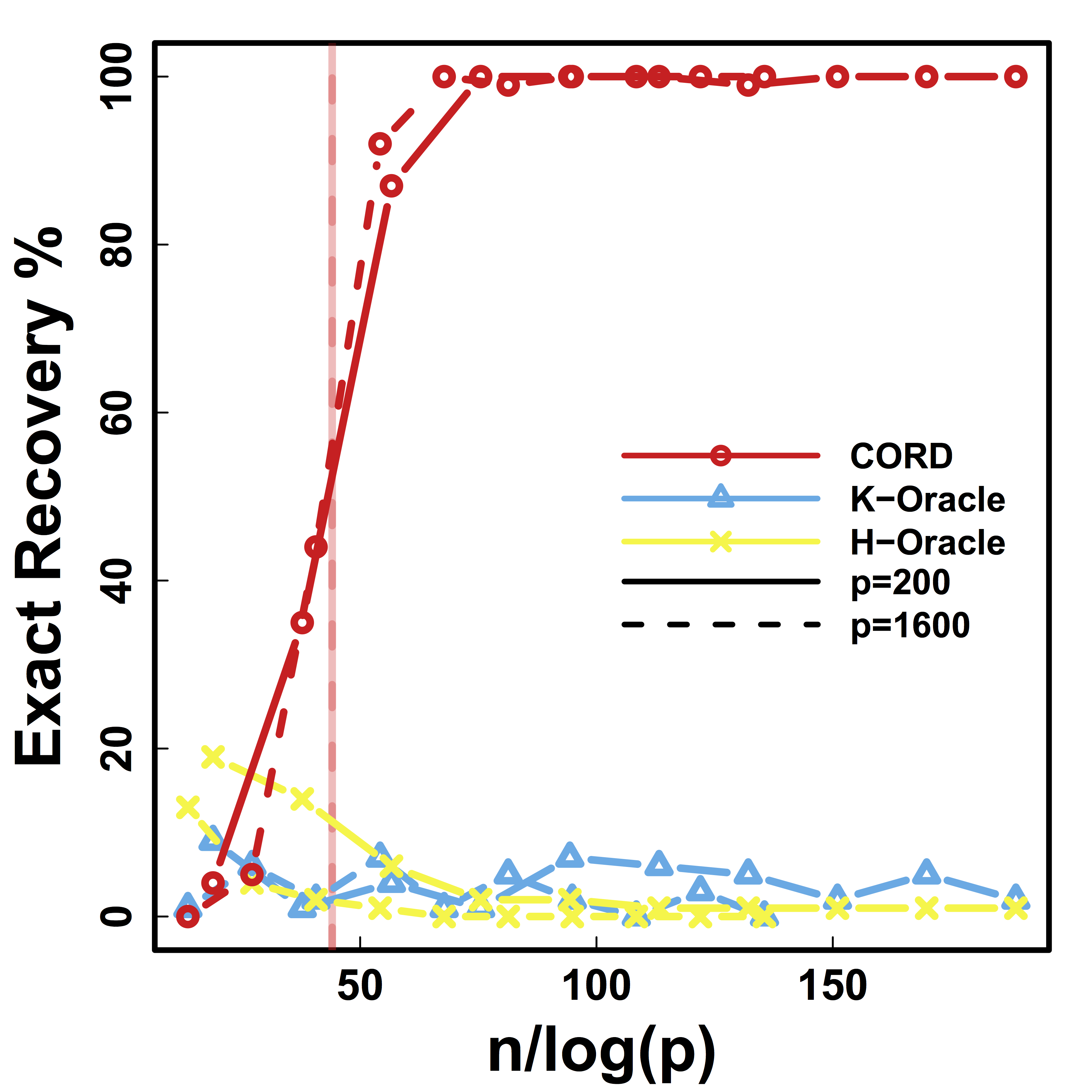
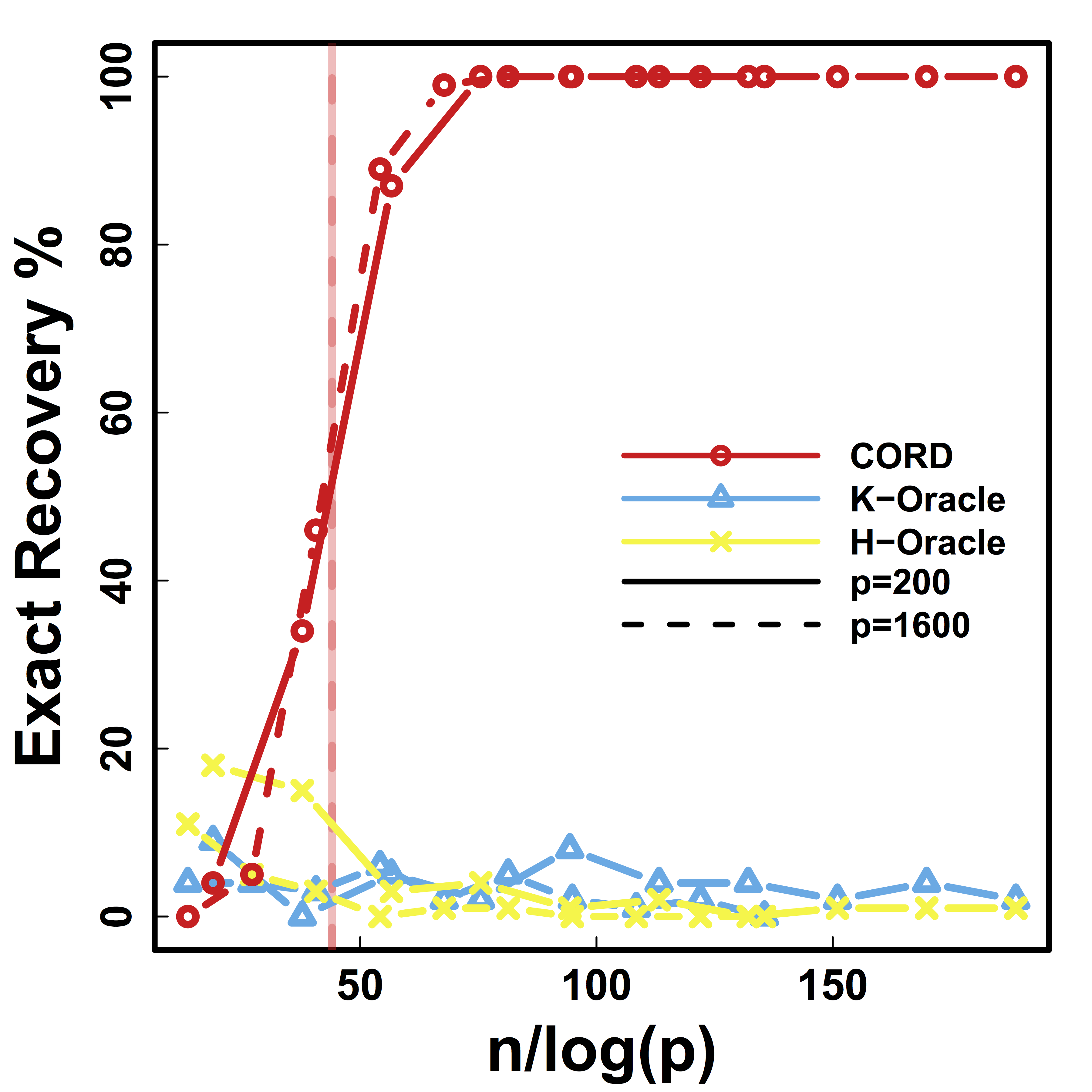
Different models for $C$="$\cov(Z)$" and $\alpha = 2 n^{-1/2} \log^{1/2} p$
Vertical lines: theoretical sample size based on our lower bound
HC and Kmeans fail even if inputting the true $K$.
Data-driven choice of $\alpha$: Averaging
- Introduce block averaging operator $\left[\varUpsilon\left(R,G\right)\right]_{ab} =$
$$\begin{cases} \left|G_{k}\right|^{-1}\left(\left|G_{k}\right|-1\right)^{-1}\sum_{i,j\in G_{k},i\ne j}R_{ij} & \mbox{if } a\ne b \mbox{ and } k=k^{\prime}\\ \left|G_{k}\right|^{-1}\left|G_{k^{\prime}}\right|^{-1}\sum_{i\in G_{k},j\in G_{k^{\prime}}}R_{ij} & \mbox{if } a\ne b \mbox{ and } k\ne k^{\prime}\\ 1 & \mbox{if }a=b. \end{cases} $$
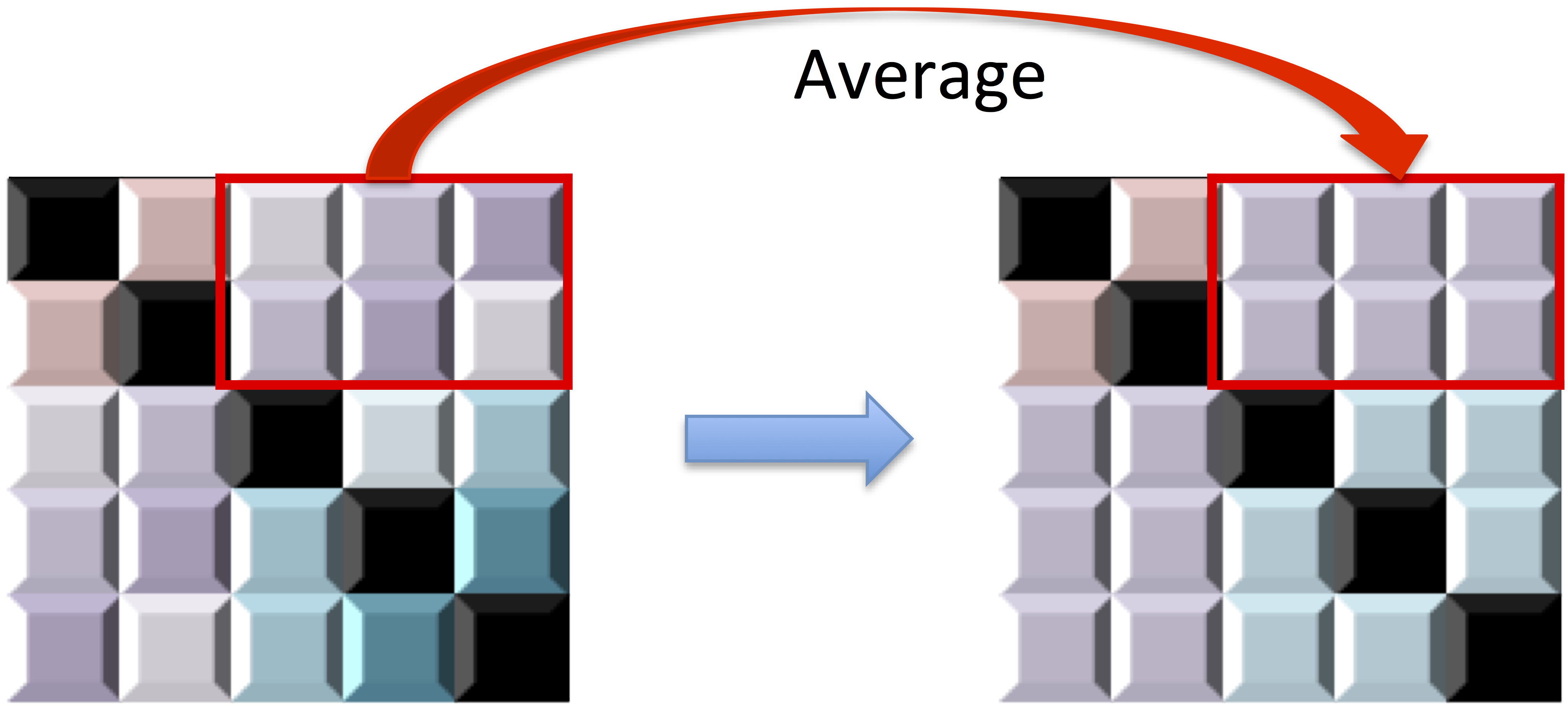
Data-driven choice of $\alpha$: Prediction
- Choose $\alpha$ via cross validation using minimization over a grid of $\alpha$: $$\min_\alpha \| \varUpsilon\left(\hat R,G_\alpha \right) - \hat{R}_{test}\|_F^2 $$
Cross Validation
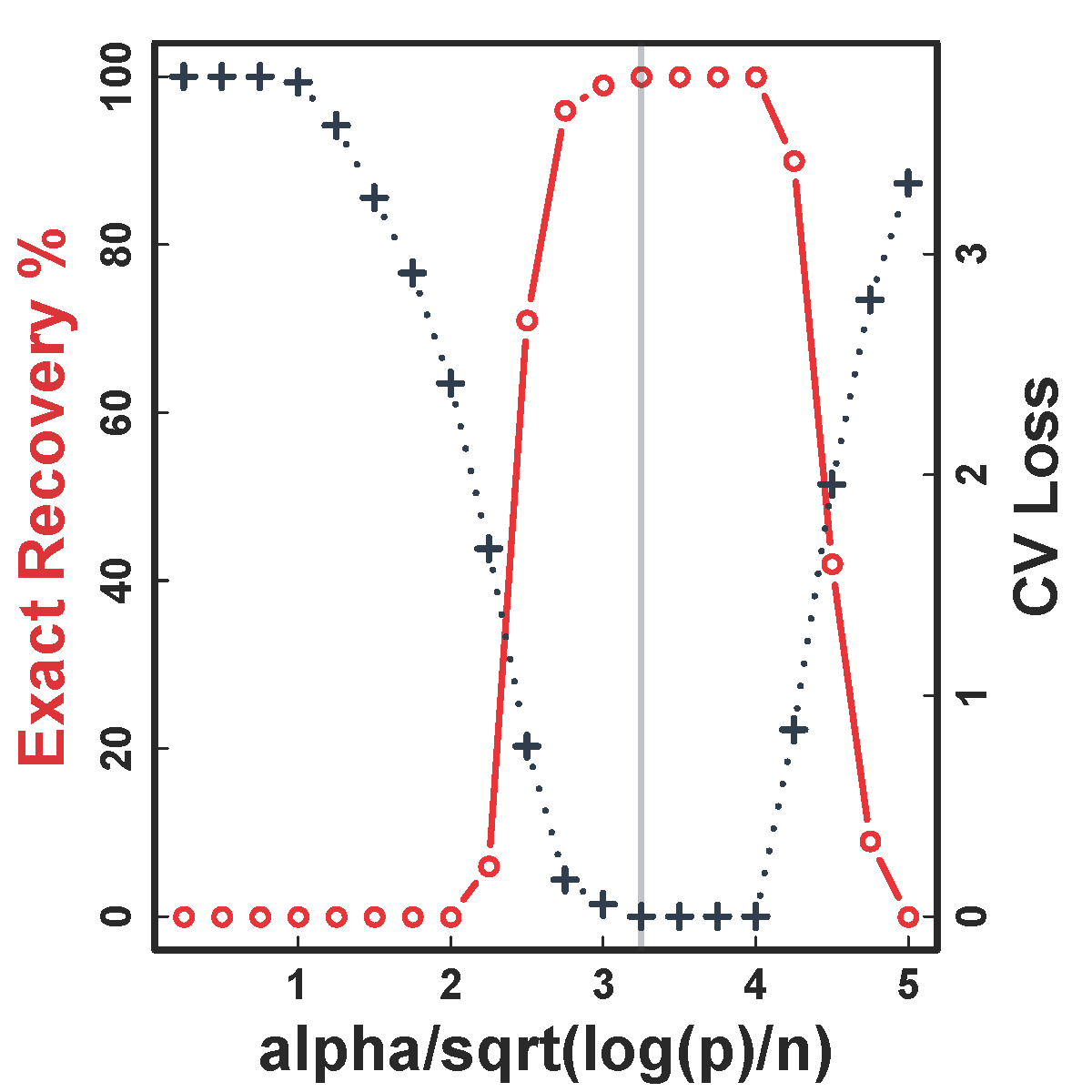
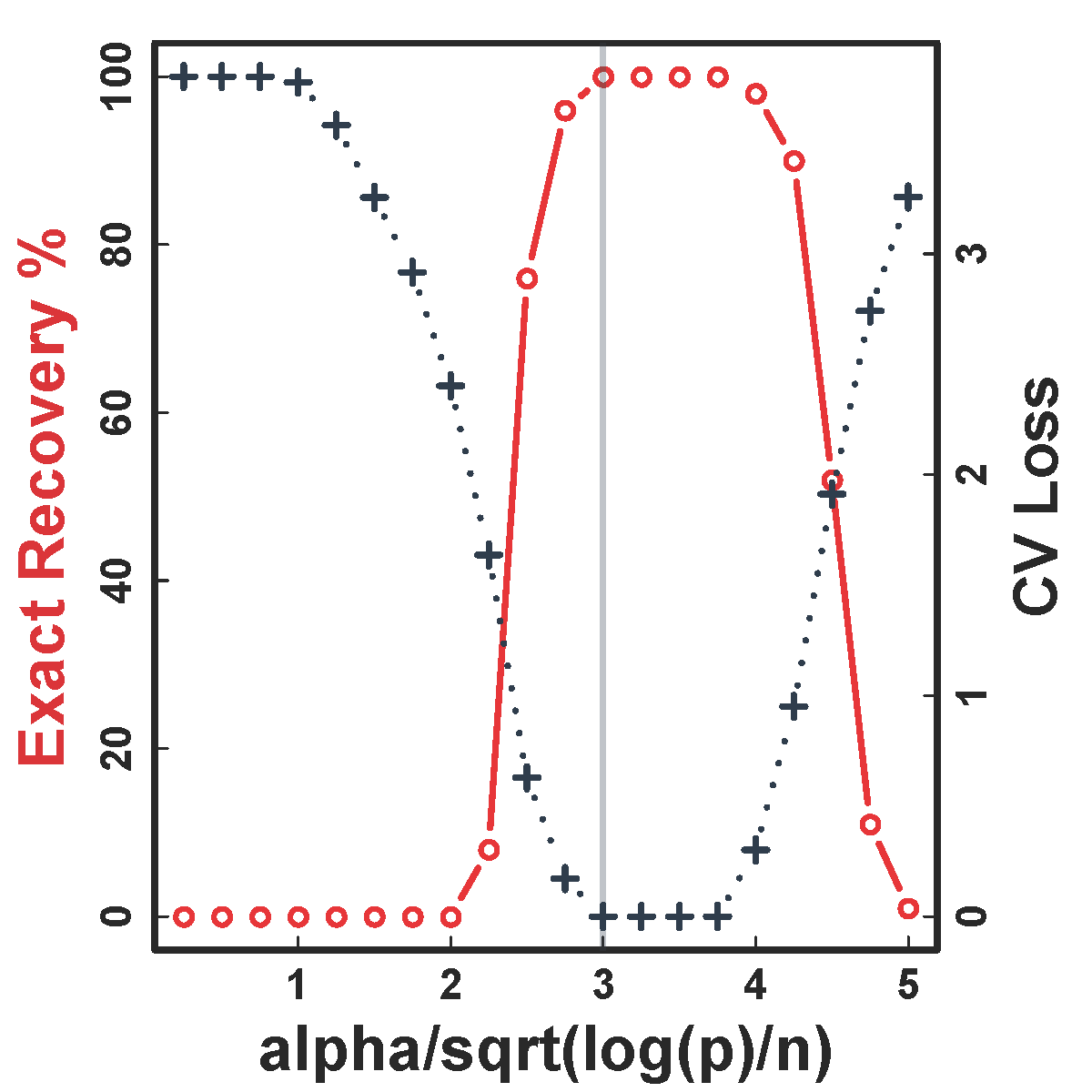
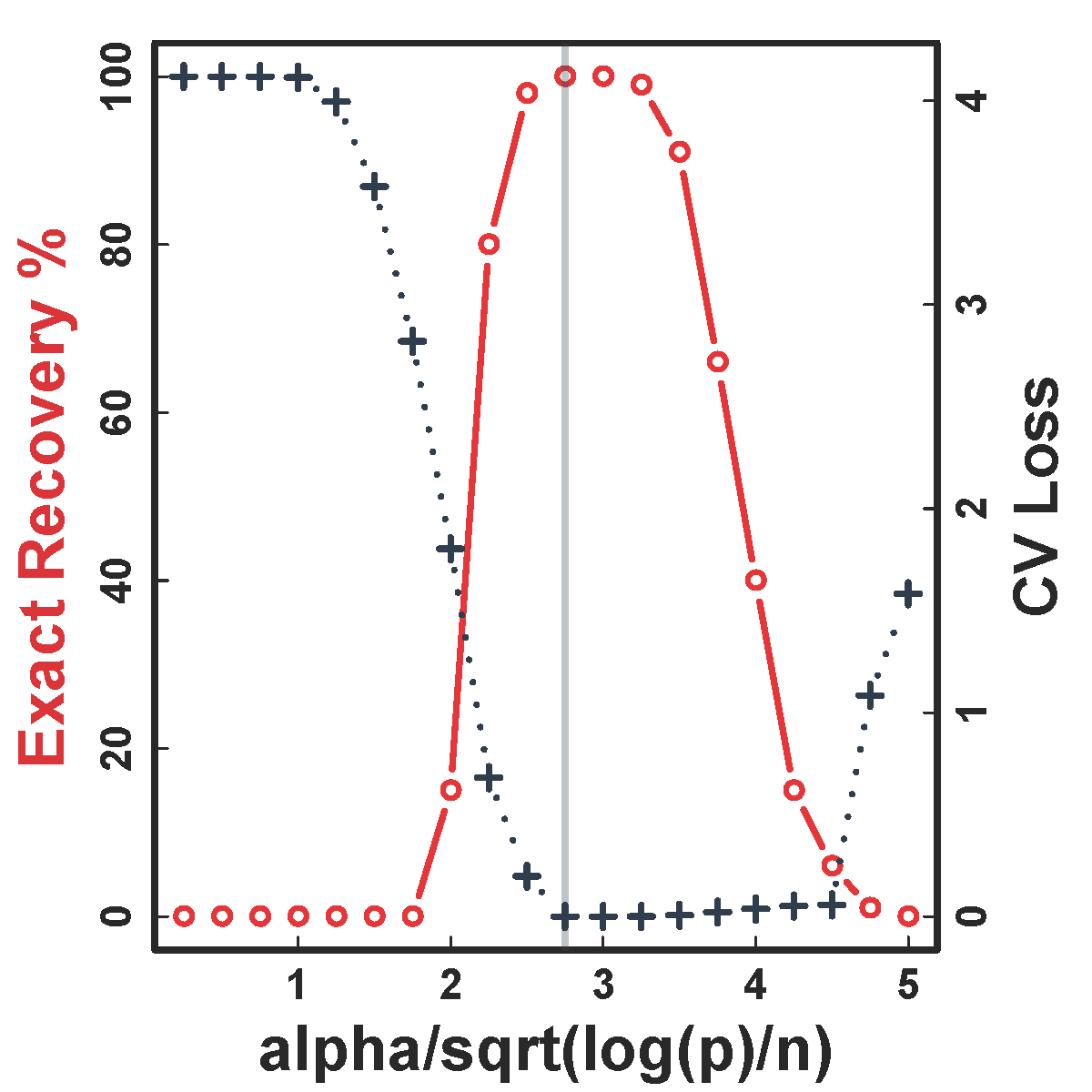
CV selects the constants to yield close to 100% recovery, as predicted by our theory (at least for large $n>200$)
Cross Validation
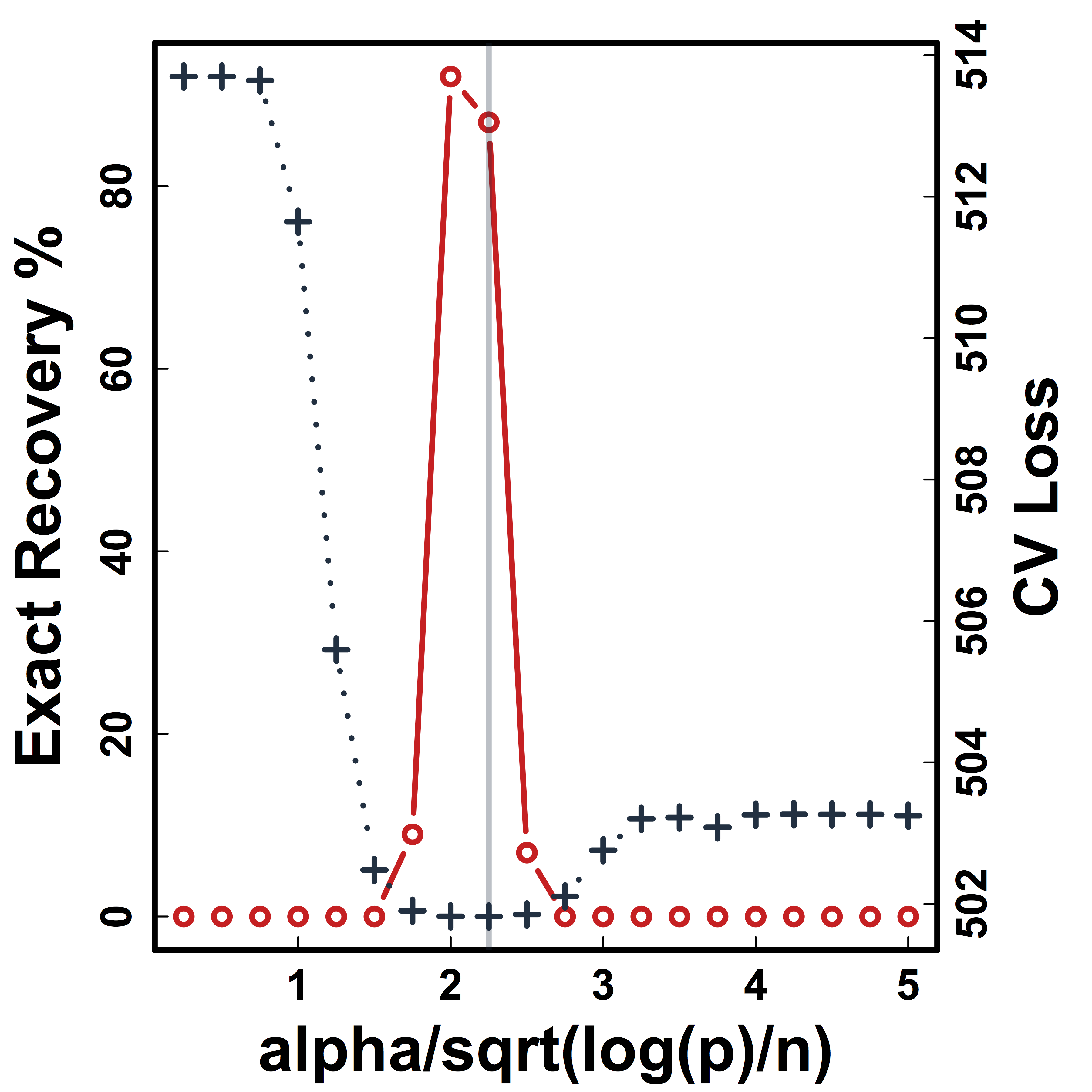
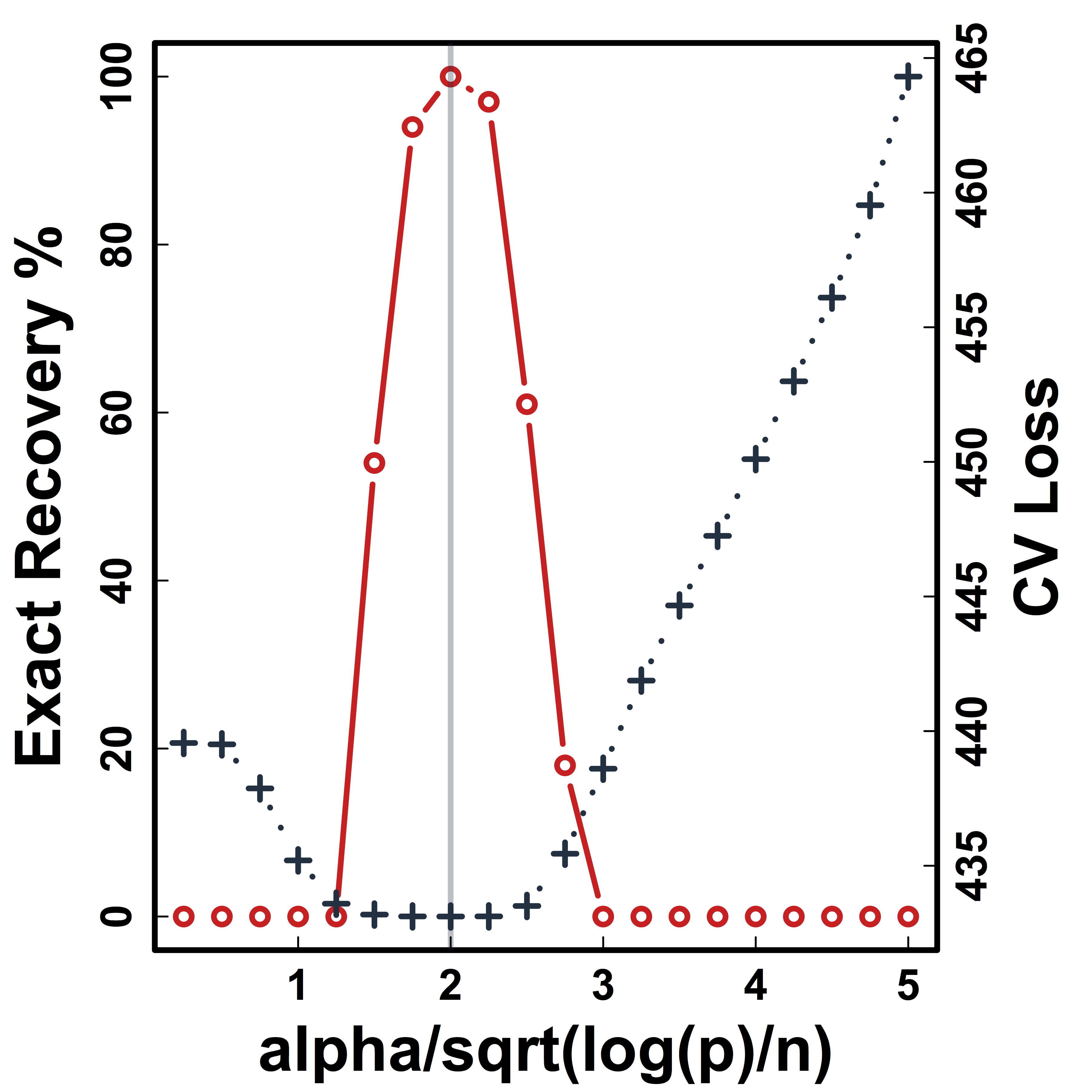
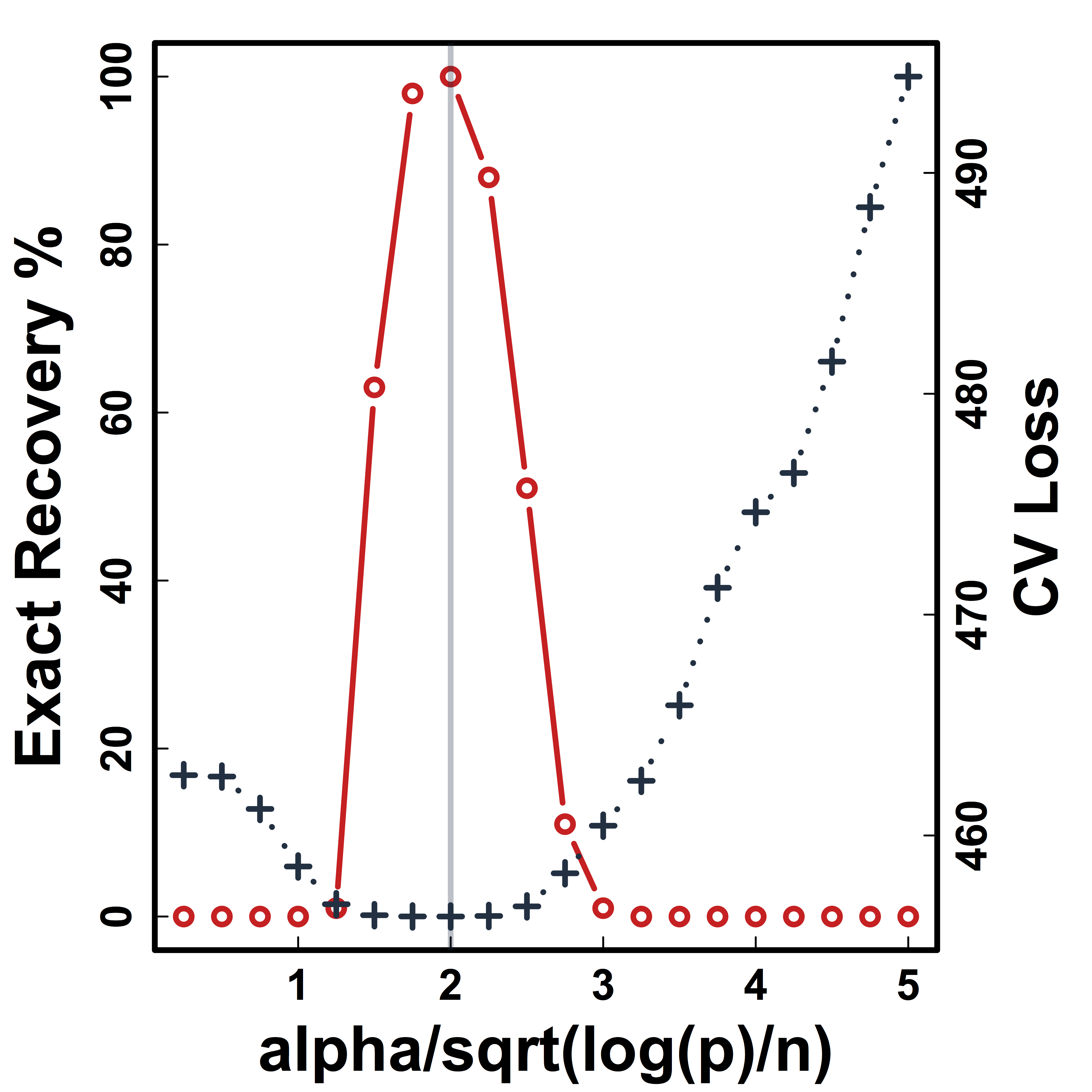
Recovery % in red and CV loss in black.
Metric Comparison: Without Threhold
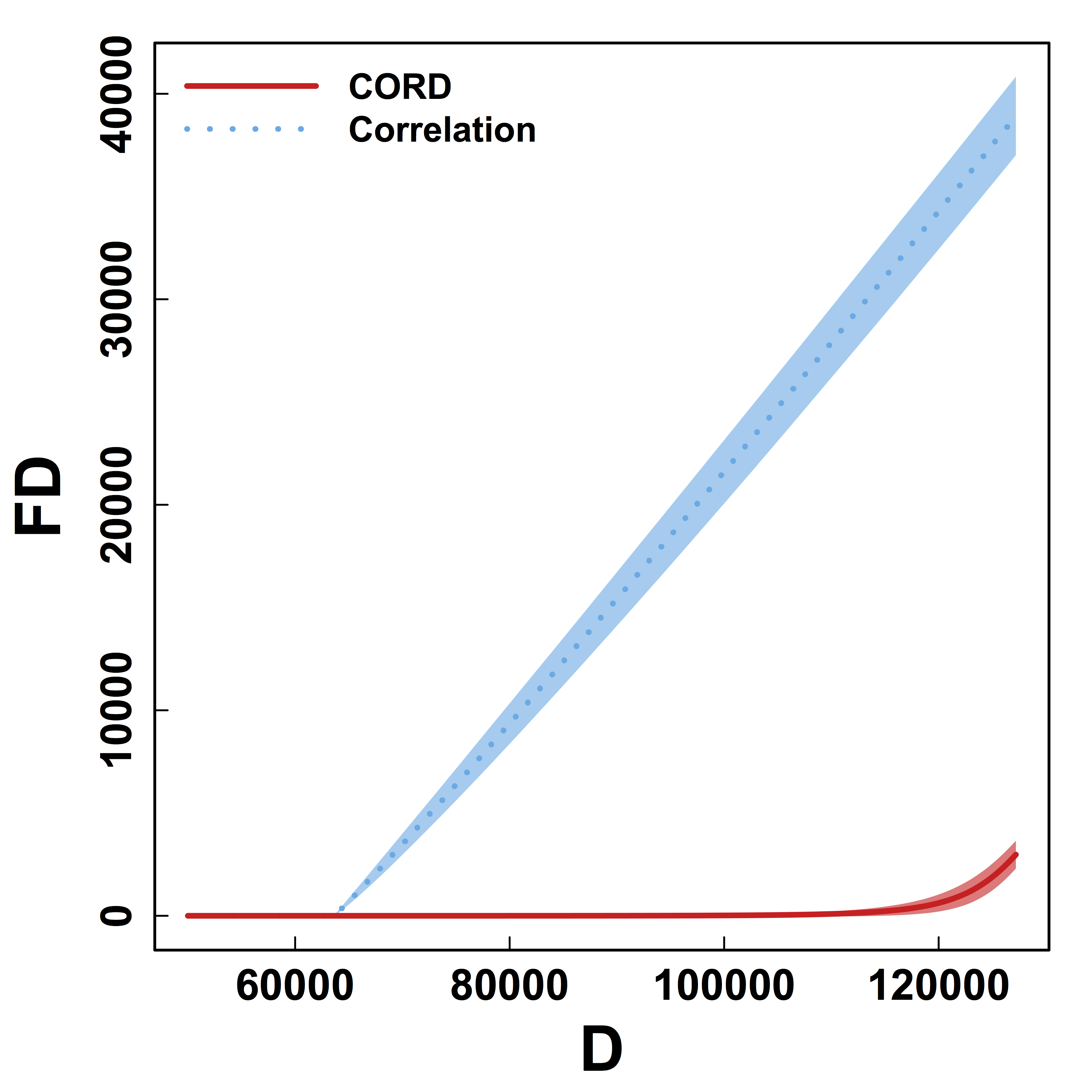
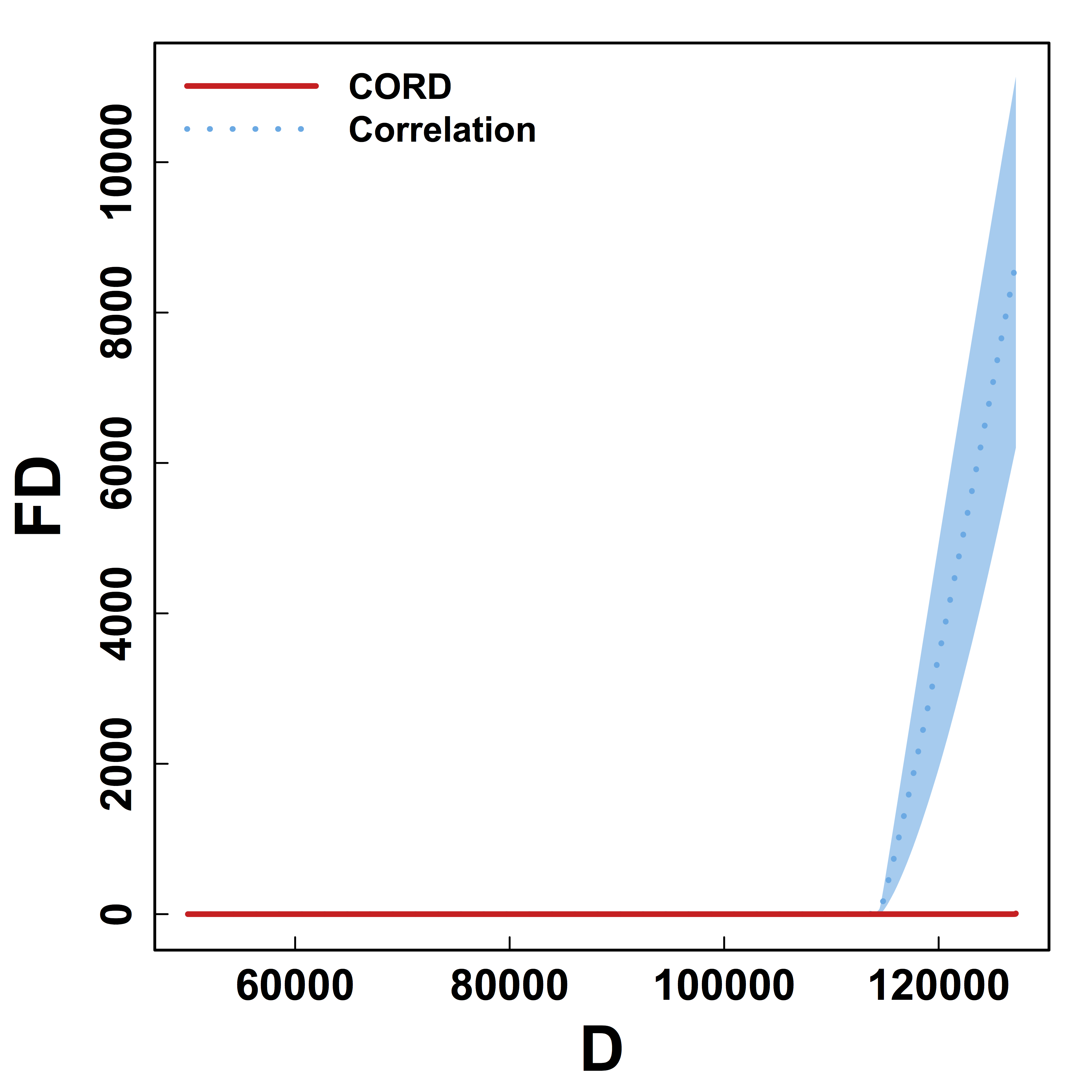
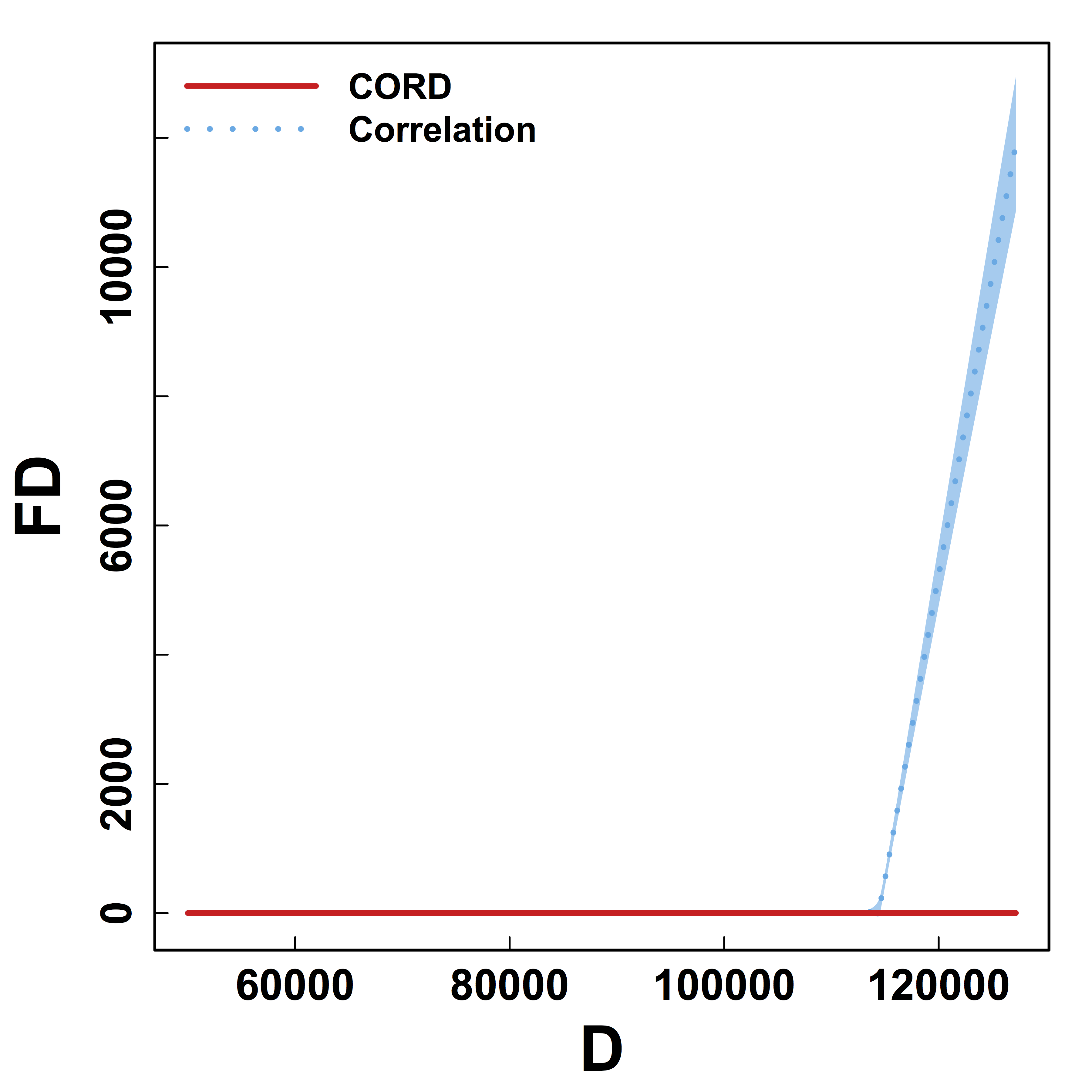
HC and Kmeans metrics yield more false discoveries (FD) as the threshold (or $K$) varies.
Real Data
fMRI Studies
Sub 1, Sess 1

Time 1

2
…

~200
⋮
Sub i, Sess j


…

⋮
Sub ~100, Sess ~4


…

This talk: one subject, two sessions (to test replicability)
Functional MRI
- fMRI matrix: BOLD from different brain regions
- Variable: different brain regions
- Sample: time series (after whitening or removing temporal correlations)
-
Clusters of brain regions
- Two data matrices from two scan sessions OpenfMRI.org
- Use Power's 264 regions/nodes
Test Prediction/Reproducibilty
- Find partitions using the first session data
- Average each block cor to improve estimation
- Compare with the cor matrix from the second scan $$ \| Avg_{\hat{G}}(\hat{\Sigma}_1) - \hat{\Sigma}_2 \|$$
- Difference is
smaller if clustering $\hat{G}$ isbetter
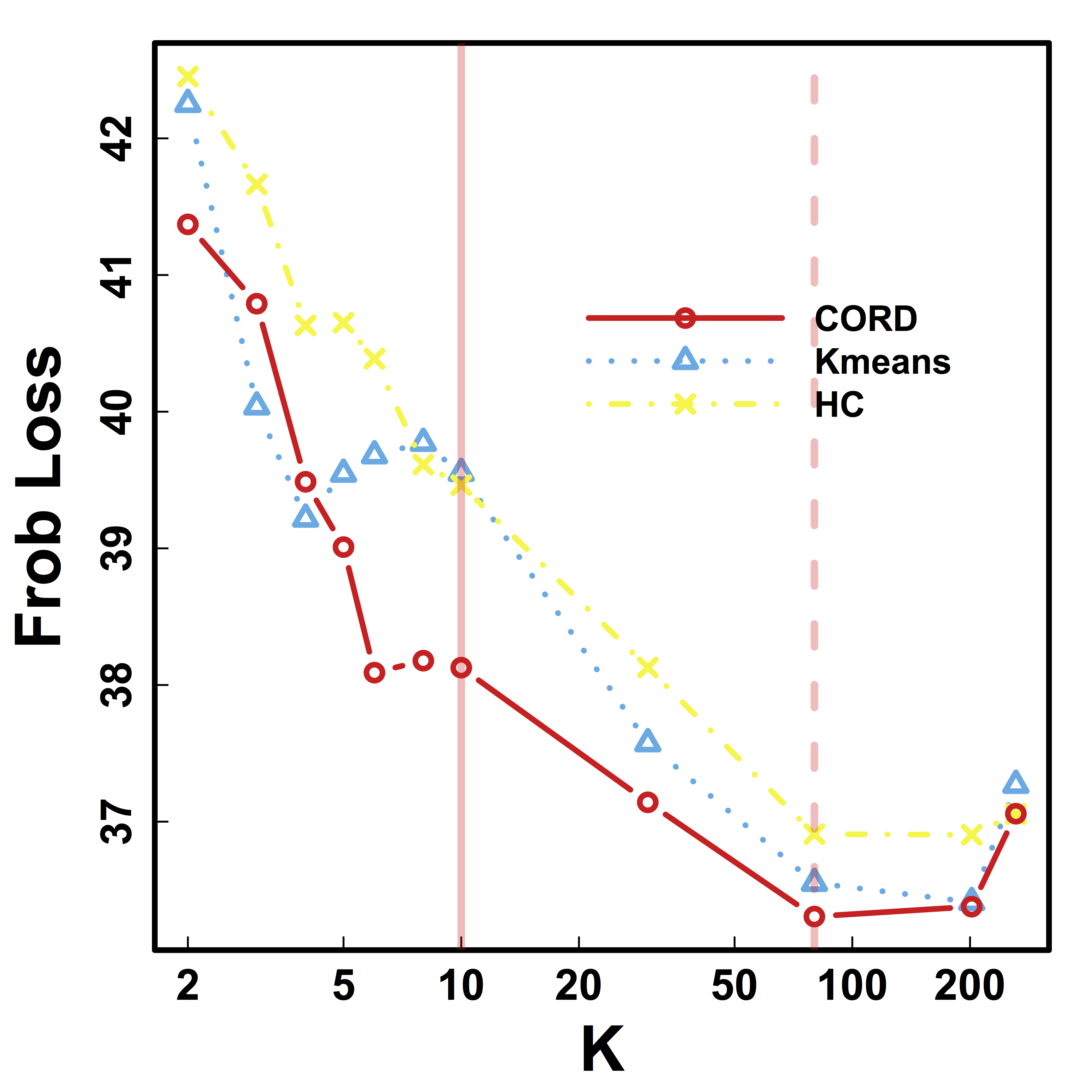
Vertical lines: fixed (solid) and data-driven (dashed) thresholds
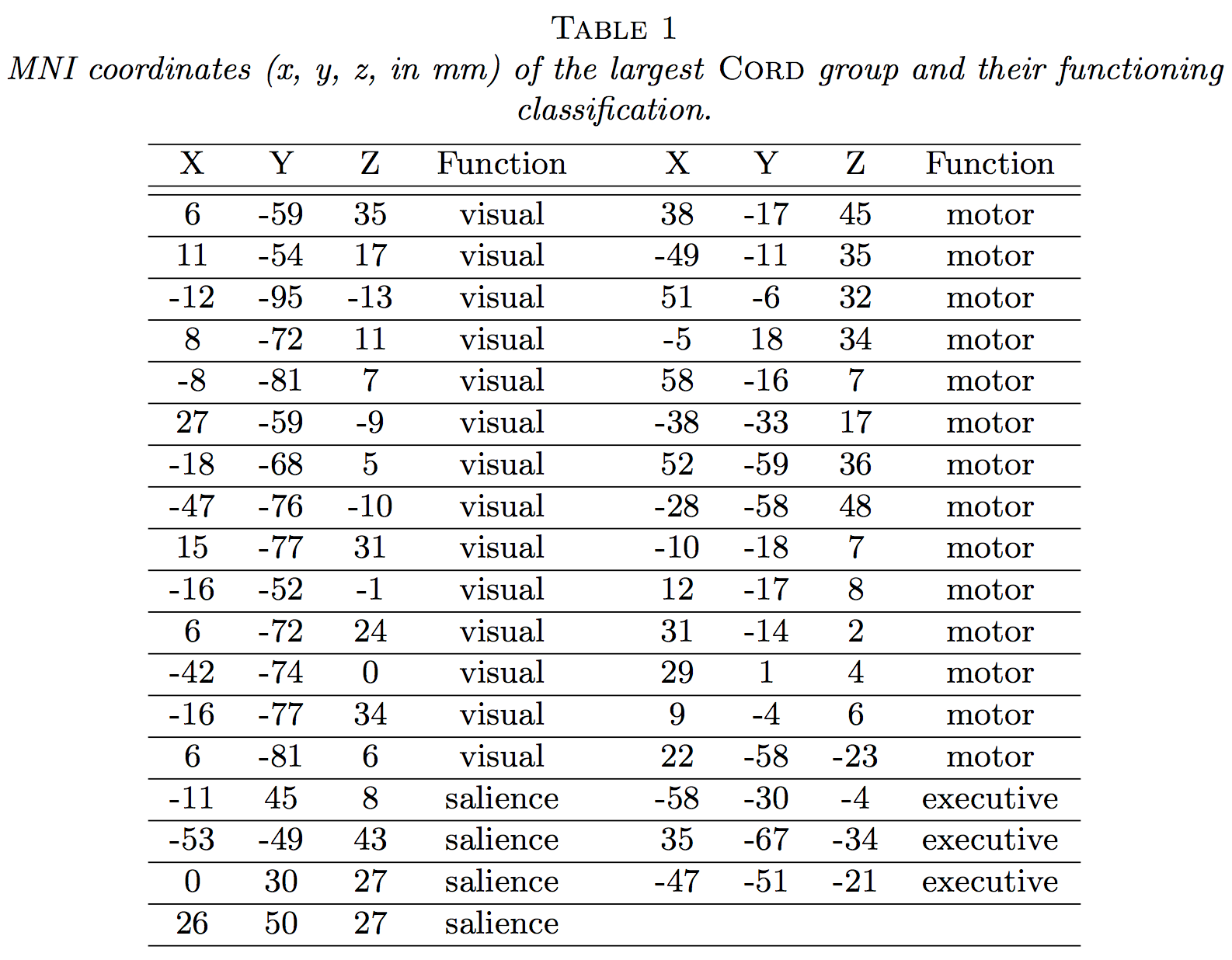
Our visual-motor task!
Discussion
- Cov + clustering = Connectivity + ROI
- Identifiability, accuracy, optimality
- $G$-models: $G$-latent, $G$-block, $G$-exchangeable
- New metric, method, and theory
- Paper: google
"cord clustering" (arXiv 1508.01939) - R package:
cord on CRAN